
分析 (1)对原式先化简,再将x=$\frac{1}{3}$代入化简后的式子即可解答本题;
(2)根据|a+b-1|+(a-b-3)2=0,可以得到a、b的值,从而可以得到-3a2(ab2+2a)+4a(-ab2)的值.
解答 解:(1)x2(2x-1)-2x(x2-2x+3)
=2x3-x2-2x3+4x2-6x
=3x2-6x,
当$x=\frac{1}{3}$时,原式=$3×(\frac{1}{3})^{2}-6×\frac{1}{3}=3×\frac{1}{9}-2=\frac{1}{3}-2$=$-\frac{5}{3}$;
(2)∵|a+b-1|+(a-b-3)2=0,
∴$\left\{\begin{array}{l}{a+b-1=0}\\{a-b-3=0}\end{array}\right.$
解得,$\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$
∴-3a2(ab2+2a)+4a(-ab2)
=-3a3b2-6a3-4a2b2
=-3×23×(-1)2-6×23-4×22×(-1)2
=-24-48-16
=-88.
点评 本题考查整式的混合运算、绝对值,解题的关键是先对原式化简,会对化简后的式子求值,注意计算过程中符号的确定.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
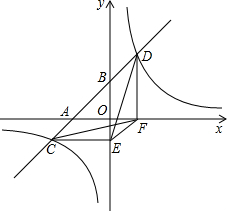 如图,直线l与x轴、y轴交于A、B两点.与双曲线y=$\frac{k}{x}$和交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F.连接CF、DE.则下列结论中:
如图,直线l与x轴、y轴交于A、B两点.与双曲线y=$\frac{k}{x}$和交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F.连接CF、DE.则下列结论中:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
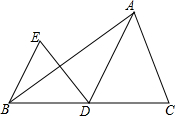 如图,AD是△ABC中BC边上的中线,∠ADC为锐角,把△ADC沿直线AD折过来,点C落在点E的位置上.试猜想直线BE与直线DA的位置关系,并证明你的猜测.
如图,AD是△ABC中BC边上的中线,∠ADC为锐角,把△ADC沿直线AD折过来,点C落在点E的位置上.试猜想直线BE与直线DA的位置关系,并证明你的猜测.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
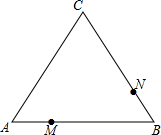 如图,在△ABC中,AB=30cm,BC=35cm,∠B=60°,有一动点M自A向B以1cm/s的速度运动,动点N自B向C以2cm/s的速度运动,若M,N同时分别从A,B出发.
如图,在△ABC中,AB=30cm,BC=35cm,∠B=60°,有一动点M自A向B以1cm/s的速度运动,动点N自B向C以2cm/s的速度运动,若M,N同时分别从A,B出发.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com