
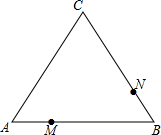
 如图,在△ABC中,AB=30cm,BC=35cm,∠B=60°,有一动点M自A向B以1cm/s的速度运动,动点N自B向C以2cm/s的速度运动,若M,N同时分别从A,B出发.
如图,在△ABC中,AB=30cm,BC=35cm,∠B=60°,有一动点M自A向B以1cm/s的速度运动,动点N自B向C以2cm/s的速度运动,若M,N同时分别从A,B出发.分析 (1)因为∠B=60°,所以当△BMN为等边三角形时,BM=BN,据此来求点M、N的运动时间;
(2)需要分类讨论:∠BMN=90°和∠BNM=90°两种情况,利用直角三角形30°的性质解决问题.
解答 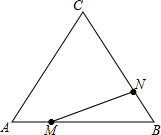 解:(1)当,△BMN为等边三角形时,BM=BN,
解:(1)当,△BMN为等边三角形时,BM=BN,
则设运动时间为t,依题意得:
30-t=2t,
解得t=10.
答:出发10秒后,△BMN为等边三角形;
(2)①当∠MNB=90°时,∵∠B=60°,
∴∠NMB=30°,
∴MB=2BN,
∴30-t=4t,
∴t=6,
②当∠NMB=90°时,∵∠B=60°,
∴∠MNB=30°,
∴BN=2BM,
∴2t=2(30-t),
∴t=15,
∴t=6或15秒时,△MNB是直角三角形.
点评 本题考查等边三角形的判定、直角三角形的判定、直角三角形30度角的性质,解题的关键是利用方程的思想解决问题,学会转化的思想,把问题转化为方程,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
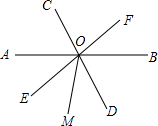 如图,直线AB,CD,EF相交于点O,∠BOD=64°,∠AOF=140°.
如图,直线AB,CD,EF相交于点O,∠BOD=64°,∠AOF=140°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com