
| A. | 0 | B. | 1 | C. | -1 | D. | i |
分析 i1=i,i2=-1,i3=i2•i=(-1)•i=-i,i4=(i2)2=(-1)2=1,i5=i4•i=i,i6=i5•i=-1,从而可得4次一循环,一个循环内的和为0,计算即可.
解答 解:由题意得,i1=i,i2=-1,i3=i2•i=(-1)•i=-i,i4=(i2)2=(-1)2=1,i5=i4•i=i,i6=i5•i=-1,
故可发现4次一循环,一个循环内的和为0,
∵$\frac{2013}{4}$=503…1,
∴i+i2+i3+i4+…+i2012+i2013=i.
故选:D.
点评 本题考查了一元二次方程的解的定义,实数的运算,解答本题的关键是计算出前面几个数的值,发现规律,求出一个循环内的和再计算,有一定难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
| 摸到白球的频率$\frac{m}{n}$ | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
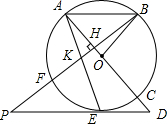 如图,AC是⊙O的直径,BF是⊙O的弦,BF⊥AC于点H,在BF上截取KB=AB,AK的
如图,AC是⊙O的直径,BF是⊙O的弦,BF⊥AC于点H,在BF上截取KB=AB,AK的查看答案和解析>>
科目:初中数学 来源: 题型:解答题
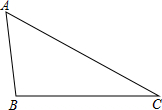 如图,在△ABC中,AB=3,BC=5,AC=6,请解答下列问题:
如图,在△ABC中,AB=3,BC=5,AC=6,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
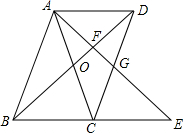 如图,?ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.
如图,?ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,对角线AC的垂直平分线EF分别与边AD、BC相交于E、F,垂足为O,连接AF、CE.
如图,在矩形ABCD中,对角线AC的垂直平分线EF分别与边AD、BC相交于E、F,垂足为O,连接AF、CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
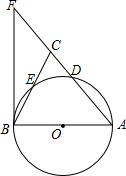 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com