
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
| 摸到白球的频率$\frac{m}{n}$ | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
分析 (1)由频率可估计概率,继而求得答案;
(2)首先可求得摸出白球的概率,然后直接利用概率公式求解即可求得答案;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与这两只球颜色不同的情况,再利用概率公式即可求得答案.
解答 解:(1)由统计图可得:当n很大时,摸到白球的频率将会接近0.25;
故答案为:0.25;
(2)∵在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共4只,且白球的概率为0.25;
∴口袋中白种颜色的球有:4×0.25=1(只);
答:估算口袋中白种颜色的球有1只;
(3)画树状图得: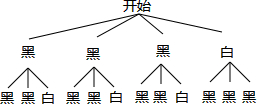
∵共有12种等可能的结果,这两只球颜色不同的有6种情况,
∴这两只球颜色不同的概率是:$\frac{6}{12}$=$\frac{1}{2}$.
点评 此题考查了列表法或树状图法求概率以及利用频率估计概率的知识.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
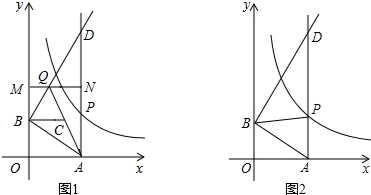
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
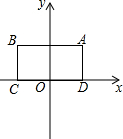 对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为($\sqrt{3}$,2),顶点C、D在x轴上,且OC=OD.
对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为($\sqrt{3}$,2),顶点C、D在x轴上,且OC=OD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
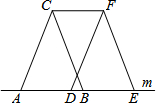 如图所示,三角形ABC沿直线m向右平移a厘米,得到三角形DEF,下列说法中错误的是( )
如图所示,三角形ABC沿直线m向右平移a厘米,得到三角形DEF,下列说法中错误的是( )| A. | AC∥DF | B. | CF∥AB | C. | CF=a厘米 | D. | BD=a厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
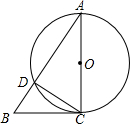 如图,AC是⊙O的直径,∠A=30°,AB交⊙O于D,CD=1,
如图,AC是⊙O的直径,∠A=30°,AB交⊙O于D,CD=1,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com