
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| d(x) | 3a-b+c | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |
分析 (1)根据新定义可以得到本问的答案;
(2)根据若m、n为正数,则d(mn)=d(m)+d(n);d($\frac{m}{n}$)=d(m)-d(n),可以解答本题;
(3)根据第二问的运算性质可以解答本题,关键是灵活变活,运用反证法说明哪些数据是正确的,从而可以得到哪两个数据是错误的,然后进行纠正即可.
解答 解:(1)根据题意可得,d(103)可表示为:10b=103,得b=3.
故答案为:3.
(2)∵若m、n为正数,则d(mn)=d(m)+d(n),d(3)=0.477
∴$\frac{{d({2^5})}}{d(2)}$=$\frac{5d(2)}{d(2)}=5$,
d(9)=d(3×3)=d(3)+d(3)=0.477+0.477=0.954,
d(0.3)=d($\frac{3}{10}$)=d(3)-d(10)=0.477-1=-0.523
故答案为:5,0.954,-0.523
(3)若d(3)≠2a-b,
则d(9)=2d(3)≠4a-2b,d(27)=3d(3)≠6a-3b,
从而表中有三个劳格数是错误的,与题设矛盾,
∴d(3)=2a-b,d(9)=4a-2b,d(27)=6a-3b都是正确的;
若d(5)≠a+c,则d(2)=d(10)-d(5)=1-d(5)≠1-a-c,
∴d(8)=3d(2)≠3-3a-3c,d(6)=d(3)+d(2)≠1+a-b-c,
表中也有三个劳格数是错误的,与题设矛盾,
∴d(5)=a+c,d(6)=1+a-b-c,d(8)=3-3a-3c都是正确的;
∴表中只有d(1.5)和d(12)的值是错误的,应纠正为:
d(1.5)=d(3)+d(5)-d(10)=3a-b+c-1,
d(12)=d(3)+2d(2)=2-b-2c.
点评 本题考查有理数的混合运算,解题的关键是明确新定义和运算性质.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
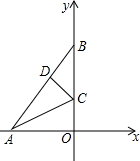 如图,平面直角坐标系中有一张三角形纸片AOB,其顶点A,B的坐标分别为A(-6,0),B(0,8),点O为坐标原点.
如图,平面直角坐标系中有一张三角形纸片AOB,其顶点A,B的坐标分别为A(-6,0),B(0,8),点O为坐标原点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com