
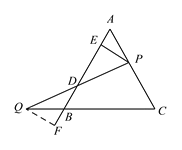
【题目】如图,在等边三角形ABC中,AB=12cm,动点P从点A出发以1cm/s的速度沿AC匀速运动,动点Q同时从点B出发以同样的速度沿CB的延长线方向匀速运动,当点P到达点C时,点P,Q同时停止运动.设运动时间为ts,过点P作PE⊥AB于点E,连接PQ交AB于点D.
⑴当t为何值时,△CPQ为直角三角形?
⑵求DE的长.
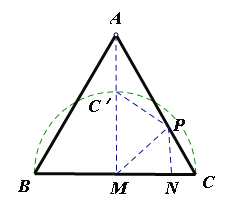
⑶取线段BC的中点M,连接PM,将△CPM沿直线PM翻折,得到△C,PM,连接AC,,当t= 时,AC,的值最小,最小值为 .

【答案】(1)4;(2)6;(3)![]() ,
,![]()
【解析】
(1)由△ABC是等边三角形,可知∠C=60°,再由CQ=2CP列式即可求得t的值;
(2)过点Q作QF⊥AB交AB的延长线于F,易证△PEA≌△QFB(AAS),则EF=AB=12cm,易证△PED≌△QFD(AAS),DE=DF,即可求得DE=![]() EF=6;
EF=6;
(3)分析可知,点![]() 的轨迹为如图所示
的轨迹为如图所示![]() ,过点P作PN⊥MN,当A,
,过点P作PN⊥MN,当A,![]() ,M三点共线时,
,M三点共线时,![]() 有最小值,再根据等边三角形性质及直角三角形性质求解即可.
有最小值,再根据等边三角形性质及直角三角形性质求解即可.
解:(1)∵△ABC是等边三角形,
∴∠C=60°,
∴当CQ=2CP时,∠CPQ=90°,
∴12+t=2(12-t),
∴t=4,
∴t=4时,△CPQ是直角三角形.
(2)如图,过点Q作QF⊥AB交AB的延长线于F,
∵PE⊥AB,
∴∠PEA=∠F=90°,
∵PA=QB,∠A=∠ABC=∠QBF=60°,
∴△PEA≌△QFB(AAS),
∴AE=BF,
∴EF=AB=12cm,
∵∠PED=∠F=90°,∠PDE=∠QDF,PE=QF,
∴△PED≌△QFD(AAS),
∴DE=DF,
∴DE=![]() EF=6.
EF=6.
(3)分析可知,点![]() 的轨迹为如图所示
的轨迹为如图所示![]() ,过点P作PN⊥MN,
,过点P作PN⊥MN,
∴当A,![]() ,M三点共线时,
,M三点共线时,![]() 有最小值,
有最小值,
∵△ABC为等边三角形,M为BC中点,
∴AM⊥BC,∠ACM=60°,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,
即当![]() 时,AC,的值最小,最小值为
时,AC,的值最小,最小值为![]() ,
,
故答案为:![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
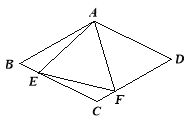
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+3.
(1)画出这个函数的图象;
(2)根据图象,直接写出;
①当函数值y为正数时,自变量x的取值范围;
②当﹣2<x<2时,函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=![]() x+
x+![]() 与y轴的交点为A,直线l1与直线l2:y=kx的交点M的坐标为M(3,a).
与y轴的交点为A,直线l1与直线l2:y=kx的交点M的坐标为M(3,a).
⑴a= ,k= ;
⑵直接写出关于x的不等式![]() x+
x+![]() ≥kx>0的解集 ;
≥kx>0的解集 ;
⑶若点B在x轴上,MB=MA,直接写出点B的坐标 .
⑷在x轴上是否存在一点N,使得NM-NA的值最大,若不存在,请说明理由;若存在,请直接写出点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜的价格随季节变化如下表,根据表中信息,下列结论错误的是( )
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
价格 | 5.00 | 5.50 | 5.00 | 4.80 | 2.00 | 1.50 | 1.00 | 0.90 | 1.50 | 3.00 | 2.50 | 3.50 |
A. ![]() 是自变量,
是自变量,![]() 是因变量
是因变量
B. 2月份这种蔬菜价格最高,为5.50元/千克
C. 2-8月份这种蔬菜价格一直在下降
D. 8-12月份这种蔬菜价格一直在上升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 是线段
是线段![]() 上的动点(点
上的动点(点![]() 与
与![]() 不重合),分别以
不重合),分别以![]() 为边向线段
为边向线段![]() 的同一侧作正
的同一侧作正![]() 和正
和正![]() .
.
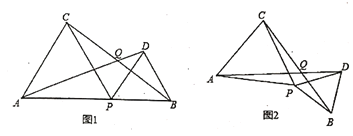
(1)请你判断![]() 与
与![]() 有怎样的数量关系?请说明理由;
有怎样的数量关系?请说明理由;
(2)连接![]() ,相交于点
,相交于点![]() ,设
,设![]() ,那么
,那么![]() 的大小是否会随点
的大小是否会随点![]() 的移动而变化?请说明理由;
的移动而变化?请说明理由;
(3)如图2,若点![]() 固定,将
固定,将![]() 绕点
绕点![]() 按顺时针方向旋转(旋转角小于
按顺时针方向旋转(旋转角小于![]() ),此时
),此时![]() 的大小是否发生变化?(只需直接写出你的猜想,不必证明)
的大小是否发生变化?(只需直接写出你的猜想,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3)+40+(﹣32)+(﹣8)
(2)12﹣(﹣18)+(﹣7)
(3)(+3![]() )﹣(﹣5
)﹣(﹣5![]() )+(﹣2
)+(﹣2![]() )﹣(﹣32
)﹣(﹣32![]() )
)
(4)81.26﹣293.8+8.74+111
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com