【题目】已知关于x的一元二次方程x2－（2m＋3）x＋m2＋2＝0。
（1）若方程有实数根，求实数m的取值范围；
（2）若方程两实数根分别为
，且满足
，求实数m的值。
【答案】（1）
；（2）2
【解析】
（1）根据方程有实数根结合根的判别式，即可得出关于m的一元一次不等式，解之即可得出结论；
（2）利用根与系数的关系可得出x1+x2=2m+3，x1x2=m2+2，结合x12+x22=31+x1x2即可得出关于m的一元二次方程，解之即可得出m的值．
解：（1）∵方程x2-（2m+3）x+m2+2=0有实数根，
∴△=[-（2m+3）]2-4（m2+2）=12m+1≥0，
解得：．
（2）∵方程x2-（2m+3）x+m2+2=0的两个根分别为x1、x2，
∴x1+x2=2m+3，x1x2=m2+2，
∵x12+x22=31+x1x2，
∴(x1+x2)2-2x1x2=31+x1x2，
即m2+12m-28=0，
解得：m1=2，m2=-14（舍去），
∴实数m的值为2．
期末宝典单元检测分类复习卷系列答案科目：初中数学 来源： 题型：
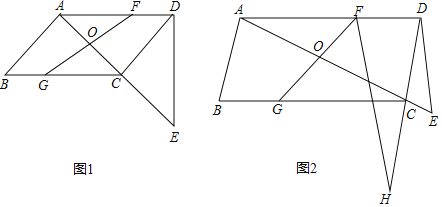
【题目】如图，在平行四边形ABCD中，AB⊥AC，过点D作DE⊥AD交直线AC于点E，点O是对角线AC的中点，点F是线段AD上一点，连接FO并延长交BC于点G．
（1）如图1，若AC＝4，cos∠CAD＝
，求△ADE的面积；
（2）如图2，点H为DC是延长线上一点，连接HF，若∠H＝30°，DE＝BG，求证：DH＝CE+
FH．
查看答案和解析>>
科目：初中数学 来源： 题型：
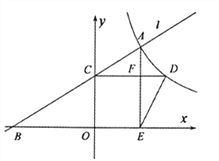
【题目】如图，已知点
是反比例函数
的图像上的一个动点，经过点的直线
交
轴负半轴于点
，交
轴正半轴于点
.过点作轴的垂线，交反比例函数的图像于点
.过点作
轴于点
，交
于点
，连接
.设点的横坐标是
.
(1)若
，求点的坐标(用含的代数式表示);
(2)若
，当四边形
是平行四边形时，求的值，并求出此时直线对应的函数表达式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有人说：“数学是思维的体操”，运用和掌握必要的“数学思想”和“数学方法”是取胜数学的重要法宝．阅读下列例题：
（1）解方程：x2﹣2|x|﹣3＝0．
解：①当x≥0时，有x2﹣2x﹣3＝0，解得x1＝﹣1（舍去），x2＝3．
②当x＜0时，有x2+2x﹣3＝0，解得x1＝1（舍去），x2＝﹣3．所以，原方程的解是x＝3或﹣3．（数学的分类讨论思想）试解方程：x2﹣|x﹣1|﹣1＝0．
（2）设a3+a﹣1＝0，求a3+a+2018的值．
解：由a3+a﹣1＝0得a3+a＝1，代入，有a3+a+2018＝1+2018＝2019（整体代入或换元思想）
试一试：当a是一元二次方程x2﹣2018x+1＝0的一个根时，求：a2﹣2017a+
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数
的图象与x轴交于两点，其中点A坐标（-1，0），点C（0，5）、D（1，8）在抛物线上，M为抛物线的顶点．
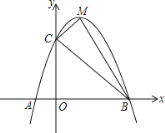
（1）求抛物线的解析式；
（2）求△MCB面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
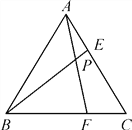
【题目】如图，等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P，且AE=CF.
(1)求证：AF=BE，并求∠FPB的度数；
(2)若AE=2，试求AP·AF的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G为AF的中点，∠ACD=2∠ACB．若DG=3，EC=1，则DE的长为（ ）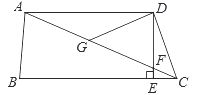
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α，将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．
（1）求证：△COD是等边三角形；
（2）当α=150°时，试判断△AOD的形状，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请阅读下列材料：
问题：已知方程x2＋x－1＝0，求一个一元二次方程，使它的根分别是已知方程根的2倍．
解：设所求方程的根为y，则y＝2x，所以x＝
.
把x＝代入已知方程，得
＋－1＝0.
化简，得y2＋2y－4＝0.
故所求方程为y2＋2y－4＝0.
这种利用方程根的代换求新方程的方法，我们称为“换根法”．
请用阅读材料提供的“换根法”求新方程(要求：把所求方程化为一般形式)：
(1)已知方程x2＋x－2＝0，求一个一元二次方程，使它的根分别是已知方程根的相反数，则所求方程为_________；
(2)已知关于x的一元二次方程ax2＋bx＋c＝0(a≠0)有两个不等于零的实数根，求一个一元二次方程，使它的根分别是已知方程根的倒数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com