
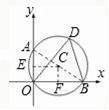
如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C在第一象限内的一点且∠ODB=60°,解答下列各题:
(1)求线段AB的长及⊙C的半径;
(2)求B点坐标及圆心C的坐标.
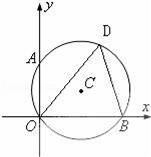

【考点】垂径定理;坐标与图形性质;勾股定理.
【分析】(1)连接AB;由圆周角定理可知,AB必为⊙C的直径;Rt△ABO中,易知OA的长,而∠OAB=∠ODB=60°,通过解直角三角形,即可求得斜边AB的长,也就求得了⊙C的半径;
(2)在Rt△ABO中,由勾股定理即可求得OB的长,进而可得到B点的坐标;过C分别作弦OA、OB的垂线,设垂足为E、F;根据垂径定理即可求出OE、OF的长,也就得到了圆心C的坐标.
【解答】解:(1)连接AB;∵∠ODB=∠OAB,∠ODB=60°
∴∠OAB=60°,
∵∠AOB是直角,
∴AB是⊙C的直径,∠OBA=30°;
∴AB=2OA=4,∴⊙C的半径r=2;
(2)在Rt△OAB中,由勾股定理得:OB2+OA2=AB2,
∴OB=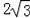
 ,∴B的坐标为:(
,∴B的坐标为:(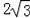
 ,0)
,0)
过C点作CE⊥OA于E,CF⊥OB于F,
由垂径定理得:OE=AE=1,OF=BF=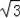
 ,
,
∴CE=
 ,CF=1,
,CF=1,
∴C的坐标为(
 ,1).
,1).

【点评】此题主要考查了圆周角定理、垂径定理、点的坐标意义、勾股定理等知识的综合应用能力,综合性较强,难度适中.


科目:初中数学 来源: 题型:
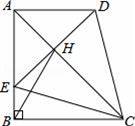
在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的是 .(填序号)
①AC⊥DE;②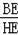
 =
=
 ;③CD=2DH;④
;③CD=2DH;④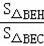
 =
=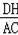
 .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
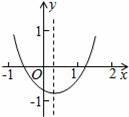
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0.
其中所有正确结论的序号是( )

A.③④ B.②③ C.①④ D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2﹣2x﹣3,AC为半圆的直径.
(1)分别求出A、B、C、D四点的坐标;
(2)求经过点D的果圆的切线DF的解析式;
(3)若经过点B的果圆的切线与x轴交于点M,求△OBM的面积.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com