
【题目】解方程
(1)![]()
(2)![]()
【答案】(1)分式方程无解;(2)x=2.
【解析】
(1)方程右边分母因式分解,两边都乘以(x+1)(x-1)去分母化为整式方程,解这个整式方程,求出x的值,将x的值代入检验,即可得到分式方程的解;
(2)方程左、右边分母因式分解后找出最简公分母x(x+3)(x-3),两边都乘以最简公分母x(x+3)(x-3)去分母化为整式方程,解这个整式方程,求出x的值,将x的值代入检验,即可得到分式方程的解.
解:(1)方程变形得:
![]() ,
,
两边同时乘以(x+1)(x-1)去分母得:
x+1=2,
解得:x=1,
当x=1时(x+1)(x-1)=0
∴x=1不是原分式方程的解;
∴原分式方程无解.
(2)方程变形得
![]()
两边同时乘以最简公分母为x(x+3)(x-3)去分母得:
7(x-3)+3(x+3)=4x,
解得:x=2,
当x=2时x(x+3)(x-3) ![]() 0,
0,
∴x=2是原分式方程的解.
∴原分式方程的解是x=2


科目:初中数学 来源: 题型:
【题目】阅读下列材料:
1637年笛卡尔在其《几何学》中,首次应用“待定系数法”将四次方程分解为两个二次方程求解,并最早给出因式分解定理.
他认为:对于一个高于二次的关于x的多项式,“![]() 是该多项式值为0时的一个解”与“这个多项式一定可以分解为(
是该多项式值为0时的一个解”与“这个多项式一定可以分解为(![]() )与另一个整式的乘积”可互相推导成立.
)与另一个整式的乘积”可互相推导成立.
例如:分解因式![]() .
.
∵![]() 是
是![]() 的一个解,∴
的一个解,∴![]() 可以分解为
可以分解为![]() 与另一个整式的乘积.
与另一个整式的乘积.
设![]()
而![]() ,则有
,则有
 ,得
,得![]() ,从而
,从而![]()
运用材料提供的方法,解答以下问题:
(1)①运用上述方法分解因式![]() 时,猜想出
时,猜想出![]() 的一个解为_______(只填写一个即可),则
的一个解为_______(只填写一个即可),则![]() 可以分解为_______与另一个整式的乘积;
可以分解为_______与另一个整式的乘积;
②分解因式![]() ;
;
(2)若![]() 与
与![]() 都是多项式
都是多项式![]() 的因式,求
的因式,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晨光文具店有一套体育用品:1个篮球,1个排球和1个足球,一套售价300元,也可以单独出售,小攀同学共有50元、20元、10元三种面额钞票各若干张.如果单独出售,每个球只能用到同一种面额的钞票去购买.若小面额的钱的张数恰等于另两种面额钱张数的乘积,那么所有可能中单独购买三个球中所用到的钱最少的一个球是___________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲、乙两公司合做,12天可以完成,共需付工费102000元;如果甲、乙两公司单独完成此项公程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元。
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,张三打算在院落种上蔬菜.已知院落为东西长为32米,南北宽为20米的长方形,为了行走方便,要修筑同样宽度的三条小路,东西两条,南北一条,余下的部分种上各类蔬菜.若每条小路的宽均为1米.
(1)求蔬菜的种植面积;
(2)若每平方米的每季蔬菜的值为3元,成本为1元,这个院落每季的产值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位向一所希望小学赠送1080件文具,现用A、B两种不同的包装箱进行包装,已知每个B型包装箱能装的文具是A型包装箱1.5倍,单独使用B型包装箱比单独使用A型包装箱可少用12个。那么A、B型包装箱每个分别可以装多少件文具?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

【答案】![]()
【解析】过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,如图所示.

∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,由 ,
,
∴△ACD≌△CBE(ASA).
设点B的坐标为(m,﹣![]() )(m<0),则E(0,﹣
)(m<0),则E(0,﹣![]() ),点D(0,3﹣m),点A(﹣
),点D(0,3﹣m),点A(﹣![]() ﹣3,3﹣m),
﹣3,3﹣m),
∵点A(﹣![]() ﹣3,3﹣m)在反比例函数y=﹣
﹣3,3﹣m)在反比例函数y=﹣![]() 上,
上,
 ,解得:m=﹣3,m=2(舍去).
,解得:m=﹣3,m=2(舍去).
∴点A的坐标为(﹣1,6),点B的坐标为(﹣3,2),点F的坐标为(﹣1,2),
∴BF=2,AF=4,
![]()
故答案为:2![]() .
.
【点睛】
过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,根据角的计算得出“∠ACD=∠CBE,∠BCE=∠CAD”,由此证出△ACD≌△CBE;再设点B的坐标为(m,﹣![]() ),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
【题型】填空题
【结束】
18
【题目】二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),下面给出了部分信息:七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82;八年级10名学生的竞赛成绩在C组中的数据是:94,90,94.
七、八年级抽取的学生竞赛成绩统计表
年级 | 七年级 | 八年级 |
平均数 | 92 | 92 |
中位数 | 93 | b |
众数 | c | 100 |
方差 | 52 | 50.4 |
根据以上信息,解答下列问题:
(1)直接写出上述图表中a,b,c的值;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校七、八年级共720人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(x≥90)的学生人数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() (2)
(2) ![]()
(3) ![]() (4)
(4) 
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ; (4)
; (4) ![]()
【解析】试题分析:(1)分子、分母分解因式后约分即可;
(2)先通分计算括号内分式的减法,然后把除法转化为乘法,分子、分母分解因式后约分即可;
(3)第二个分式分子、分母分解因式后约分,然后通分转化为同分母分式,最后依照同分母分式的加减法则计算即可;
(4)先通分计算括号内分式的减法,然后把除法转化为乘法,分子、分母分解因式后约分即可.
试题解析:
解:(1)原式=
=![]() ;
;
(2)原式=![]()
=![]()
=![]() ;
;
(3)原式=![]()
=![]()
=![]()
=![]()
=![]() ;
;
(4)原式=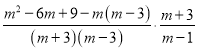
=![]()
=![]() .
.
点睛:此题考查了分式的混合运算,熟练掌握运算法则和运算顺序是解本题的关键.
【题型】解答题
【结束】
20
【题目】解分式方程:
(1) ![]() (2)
(2) ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com