
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,∠PCQ=45°,把∠PCQ绕点C旋转,在整个旋转过程中,过点A作AD⊥CP,垂足为D,直线AD交CQ于E.
(1)如图①,当∠PCQ在∠ACB内部时,求证:AD+BE=DE;
(2)如图②,当CQ在∠ACB外部时,则线段AD、BE与DE的关系为_____;
(3)在(1)的条件下,若CD=6,S△BCE=2S△ACD,求AE的长.

【答案】(1)见解析 (2)AD=BE+DE (3)8
【解析】试题分析:(1)延长DA到F,使DF=DE,根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得证;
(2)在AD上截取DF=DE,然后根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得到AD=BE+DE;
(3)根据等腰直角三角形的性质求出CD=DF=DE,再根据等高的三角形的面积的比等于底边的比求出AF=2AD,然后求出AD的长,再根据AE=AD+DE代入数据进行计算即可得解.
试题解析:(1)证明:如图①,延长DA到F,使DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ACD+∠ACF=∠DCF=45°.又∵∠ACB=90°,∠PCQ=45°,∴∠ACD+∠BCE=90°﹣45°=45°,∴∠ACF=∠BCE.在△ACF和△BCE中,∵ ,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD+BE=AD+AF=DF=DE,即AD+BE=DE;
,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD+BE=AD+AF=DF=DE,即AD+BE=DE;
(2)解:如图②,在AD上截取DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=∠DCE+∠DCF=90°,∴∠BCE+∠BCF=∠ECF=90°.又∵∠ACB=90°,∴∠ACF+∠BCF=90°,∴∠ACF=∠BCE.在△ACF和△BCE中,∵ ,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD=AF+DF=BE+DE,即AD=BE+DE;
,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD=AF+DF=BE+DE,即AD=BE+DE;
故答案为:AD=BE+DE.
(3)∵∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=45°+45°=90°,∴△ECF是等腰直角三角形,∴CD=DF=DE=6.∵S△BCE=2S△ACD,∴AF=2AD,∴AD=![]() ×6=2,∴AE=AD+DE=2+6=8.
×6=2,∴AE=AD+DE=2+6=8.



 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
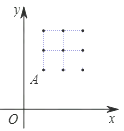
【题目】如图所示,每个小正方形的边长为1个单位长度.
(1)作出△ABC关于原点对称的△A1B1C1,并写出A1,B1,C1的坐标.
(2)y轴上有一点Q,使AQ+CQ的值最小,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标第中有一个2×2的正方形网格,每个格点的横、纵坐标均为整数,已知点A(1,2).作直线OA并向右平移k个单位,要使分布在平移后的直线两侧的格点数相同,则k的值为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,,商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,结合题意写出当x取何值时,商场获利润不少于2160元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系,根据图象,下列信息错误的是( )

A.小明看报用时8分钟
B.公共阅报栏距小明家200米
C.小明离家最远的距离为400米
D.小明从出发到回家共用时16分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=2x+a与y=-x+b的图象都经过点A(-2,0)且与y轴分别交于B,C两点

(1)分别求出这两个一次函数的解析式
(2)求△ABC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠NMA的度数是 度.
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com