
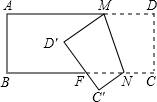
 如图,把一张长方形纸片折叠后,点D、C分别落在Dˊ,Cˊ的位置.若∠AMDˊ=32°,则∠NFDˊ等于( )
如图,把一张长方形纸片折叠后,点D、C分别落在Dˊ,Cˊ的位置.若∠AMDˊ=32°,则∠NFDˊ等于( )| A. | 148° | B. | 108° | C. | 79° | D. | 122° |
分析 如图,首先运用翻折变换的性质证明∠D′MN=∠DMN,∠MNC′=∠MNC,借助∠AMD′=32°,求出∠DMN的度数,进而求出∠MNC、∠FNC′的度数;运用三角形外角的性质,即可解决问题.
解答  解:如图,∵四边形ABCD为矩形,
解:如图,∵四边形ABCD为矩形,
∴MD∥FN,∠DMN=∠MNF;
由题意得:∠D′MN=∠DMN,∠MNC′=∠MNC,
∵∠AMD′=32°,
∴∠DMN=$\frac{180°-32°}{2}$=74°,
∴∠MNC=180°-74°=106°,∠MNF=∠DMN=74°,
∴∠FNC′=106°-74°=32°,
∴∠NFD′=90°+32°=122°,
故选D.
点评 该题主要考查了翻折变换的性质、矩形的性质、直角三角形的性质等几何知识点及其应用问题;应牢固掌握翻折变换的性质、矩形的性质等几何知识点,这是灵活运用、解题的基础和关键.


科目:初中数学 来源: 题型:选择题
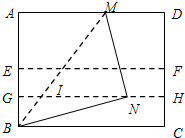 如图,对折矩形纸片ABCD,使BC与AD重合,折痕为EF,把纸片展平;再一次折叠纸片,使BC与EF重合,折痕为GH,把纸片展平;再一次折叠纸片,使点A落在GH上的点N处,并使折痕经过点B,折痕BM交GH于点I.若AB=4cm,则GI的长为( )
如图,对折矩形纸片ABCD,使BC与AD重合,折痕为EF,把纸片展平;再一次折叠纸片,使BC与EF重合,折痕为GH,把纸片展平;再一次折叠纸片,使点A落在GH上的点N处,并使折痕经过点B,折痕BM交GH于点I.若AB=4cm,则GI的长为( )| A. | $\frac{\sqrt{10}}{4}$cm | B. | $\frac{3}{4}$cm | C. | $\frac{4}{5}$cm | D. | $\frac{\sqrt{15}}{5}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x+3 | B. | y=-x+1 | C. | $y=\frac{1}{x}$ | D. | $y=-\frac{1}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com