
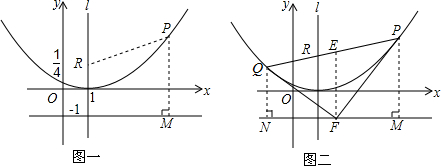
分析 (1)设顶点式y=a(x-1)2,然后把(0,$\frac{1}{4}$)代入求出a即可;
(2)根据二次函数图象上点的坐标,设P(x,$\frac{1}{4}$(x-1)2),易得PM=$\frac{1}{4}$(x-1)2+1,然后利用两点的距离公式计算PR,得到PR2=(x-1)2+[$\frac{1}{4}$(x-1)2-1]2,接着根据完全平方公式变形可得PR2=[$\frac{1}{4}$(x-1)2+1]2,则PR=$\frac{1}{4}$(x-1)2+1,所以PR=PM,于是可判断点P到R的距离与点P到直线y=-1的距离恒相等;
(3)根据(2)的结论得到得QN=QR,PR=PM,则PQ=PR+QR=PM+QN,再证明EF为梯形PMNQ的中位线,所以EF=$\frac{1}{2}$(QN+PM),则EF=$\frac{1}{2}$PQ=EQ=EP,根据点与圆的位置关系得到点F在以PQ为直径的圆上,则根据圆周角定理得∠PFQ=90°,即有PF⊥QF.
解答 (1)解:设抛物线解析式为y=a(x-1)2,
把(0,$\frac{1}{4}$)代入得a=$\frac{1}{4}$,
所以抛物线解析式为y=$\frac{1}{4}$(x-1)2;
(2)证明:如图1,设P(x,$\frac{1}{4}$(x-1)2),则PM=$\frac{1}{4}$(x-1)2+1,
∵PR2=(x-1)2+[$\frac{1}{4}$(x-1)2-1]2=(x-1)2+[$\frac{1}{4}$(x-1)]4-$\frac{1}{2}$(x-1)2+1=[$\frac{1}{4}$(x-1)]4+$\frac{1}{2}$(x-1)2+1=[$\frac{1}{4}$(x-1)2+1]2,
∴PR=$\frac{1}{4}$(x-1)2+1,
∴PR=PM,
即点P到R的距离与点P到直线y=-1的距离恒相等;
(3)证明:由(2)得QN=QR,PR=PM,
∴PQ=PR+QR=PM+QN,
∵EF⊥MN,QN⊥MN,PM⊥MN,
而E为线段PQ的中点,
∴EF为梯形PMNQ的中位线,
∴EF=$\frac{1}{2}$(QN+PM),
∴EF=$\frac{1}{2}$PQ,
∴EF=EQ=EP,
∴点F在以PQ为直径的圆上,
∴∠PFQ=90°,
∴PF⊥QF.
点评 本题考查了二次函数综合题:熟练掌握二次函数图象上点的坐标特征和梯形的中位线性质;理解坐标与图形性质;会利用待定系数法求二次函数解析式和利用两点间的距离公式计算线段的长.要充分运用(2)的结论解决(3)中的问题.


科目:初中数学 来源: 题型:选择题
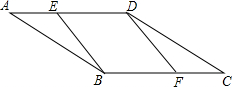 如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )| A. | AE=CF | B. | BE=DF | C. | ∠EBF=∠FDE | D. | ∠BED=∠BFD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
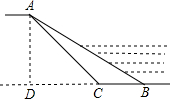 为了全面推进环境综合整治工作,某村计划对一条800m长淤积的河道进行清理,已知这条河一边在清理前迎水坡AB的长度为12m,它的坡度为1:$\sqrt{3}$,计划清理后迎水坡AC的坡角为45°,求这条河一边需清理的土方量是多少?
为了全面推进环境综合整治工作,某村计划对一条800m长淤积的河道进行清理,已知这条河一边在清理前迎水坡AB的长度为12m,它的坡度为1:$\sqrt{3}$,计划清理后迎水坡AC的坡角为45°,求这条河一边需清理的土方量是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
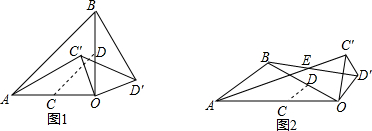
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
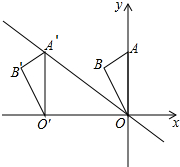 如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线y=-$\frac{3}{4}$x上,则点B与其对应点B′间的距离为8.
如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线y=-$\frac{3}{4}$x上,则点B与其对应点B′间的距离为8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
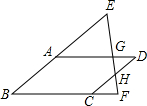 如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )| A. | $\frac{EA}{BE}$=$\frac{EG}{EF}$ | B. | $\frac{EG}{GH}$=$\frac{AG}{GD}$ | C. | $\frac{AB}{AE}$=$\frac{BC}{CF}$ | D. | $\frac{FH}{EH}$=$\frac{CF}{AD}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com