
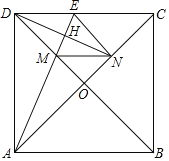
【题目】如图,已知在正方形ABCD中,对角线AC与BD交于点O,点M在线段OD上,联结AM并延长交边DC于点E,点N在线段OC上,且ON=OM,联结DN与线段AE交于点H,联结EN、MN.
(1)如果EN∥BD,求证:四边形DMNE是菱形;
(2)如果EN⊥DC,求证:AN2=NCAC.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据正方形性质及ON=OM,求出MN∥CD,进而得出四边形DMNE是平行四边形,在证明出△AOM≌△DON即可得到平行四边形DMNE是菱形;
(2)根据MN∥CD得到![]() ,再由EN⊥DC得到EN∥AD,
,再由EN⊥DC得到EN∥AD,![]() ,再由AB∥DC,得到
,再由AB∥DC,得到![]() ,即可得到
,即可得到![]() ,即为所求.
,即为所求.
证明:(1)如图1,
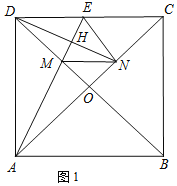
∵四边形ABCD是正方形,
∴OA=OB=OC=OD,AC⊥BD,
∵ON=OM,
∴![]() ,
,
∴MN∥CD,
又∵EN∥BD,
∴四边形DMNE是平行四边形,
在△AOM和△DON中,
∵∠AOM=∠DON=90°,OA=OD,OM=ON,
∴△AOM≌△DON(SAS),
∴∠OMA=∠OND,
∵∠OAM+∠OMA=90°,
∴∠OAM+∠OND=90°
∴∠AHN=90°.
∴DN⊥ME,
∴平行四边形DMNE是菱形;
(2)如图2,
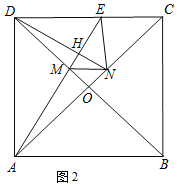
∵MN∥CD,
∴![]() ,
,
∵四边形ABCD是正方形,
∴AB∥DC,AB=DC,∠ADC=90°,
∴AD⊥DC,
又∵EN⊥DC,
∴EN∥AD,
∴![]() ,
,
∵AB∥DC,
∴![]() ,
,
∴![]() ,
,
∴AN2=NCAC.


科目:初中数学 来源: 题型:
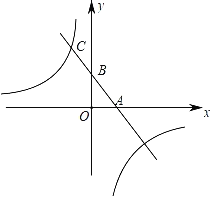
【题目】如图,在平面直角坐标系xOy中,直线y=kx+3与x,y轴分别交于点A、B,与双曲线y=![]() 交于点C(a,6),已知△AOB的面积为3,求直线与双曲线的表达式.
交于点C(a,6),已知△AOB的面积为3,求直线与双曲线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等腰三角形纸片沿图中虚线剪成四块图形,用这四块图形进行拼接,恰能拼成一个没有缝隙的正方形,则正方形的边长与等腰三角形的底边长的比为( )
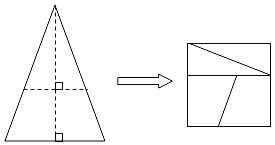
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AD=2,AB=a,点E为AD的中点,连接BE.过BE的中点F作FG⊥BE,交射线BC于点G,交边CD于H点.
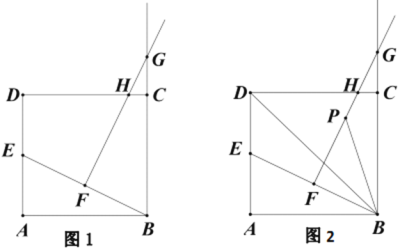
(1)连接HE、HB
①求证:HE=HB;
②若a=4,求CH的长.
(2)连接EG,△BEG面积为S
①BE= (用含a的代数式表示);
②求S与a的函数关系式.
(3)如图2,设FG的中点为P,连接PB、BD.猜想∠GBP与∠DBE的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=5cm,cosB![]() .动点D从点A出发沿着射线AC的方向以每秒1cm的速度移动,动点E从点B出发沿着射线BA的方向以每秒2cm的速度移动.已知点D和点E同时出发,设它们运动的时间为t秒.联结BD.
.动点D从点A出发沿着射线AC的方向以每秒1cm的速度移动,动点E从点B出发沿着射线BA的方向以每秒2cm的速度移动.已知点D和点E同时出发,设它们运动的时间为t秒.联结BD.
(1)当AD=AB时,求tan∠ABD的值;
(2)以A为圆心,AD为半径画⊙A;以点B为圆心、BE为半径画⊙B.讨论⊙A与⊙B的位置关系,并写出相对应的t的值.
(3)当△BDE为直角三角形时,直接写出tan∠CBD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
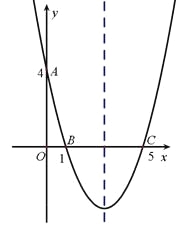
(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某湖边健身步道全长1500米,甲、乙两人同时从同一起点匀速向终点步行.甲先到达终点后立刻返回,在整个步行过程中,甲、乙两人间的距离y(米)与出发的时间x(分)之间的关系如图中OA﹣AB折线所示.
(1)用文字语言描述点A的实际意义;
(2)求甲、乙两人的速度及两人相遇时x的值.
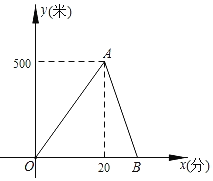
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com