
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬AB=5cm��cosB![]() ������D�ӵ�A������������AC�ķ�����ÿ��1cm���ٶ��ƶ�������E�ӵ�B������������BA�ķ�����ÿ��2cm���ٶ��ƶ�����֪��D�͵�Eͬʱ�������������˶���ʱ��Ϊt�룮����BD��
������D�ӵ�A������������AC�ķ�����ÿ��1cm���ٶ��ƶ�������E�ӵ�B������������BA�ķ�����ÿ��2cm���ٶ��ƶ�����֪��D�͵�Eͬʱ�������������˶���ʱ��Ϊt�룮����BD��
��1����AD=ABʱ����tan��ABD��ֵ��
��2����AΪԲ�ģ�ADΪ�뾶����A���Ե�BΪԲ�ġ�BEΪ�뾶����B��������A����B��λ�ù�ϵ����д�����Ӧ��t��ֵ��
��3������BDEΪֱ��������ʱ��ֱ��д��tan��CBD��ֵ��

���𰸡���1��2����2��������Բ����ʱ��![]() ��������Բ����ʱ��
��������Բ����ʱ��![]() ��������Բ�ཻʱ��
��������Բ�ཻʱ��![]() ��������Բ����ʱ��t=5��������Բ�ں�ʱ��t��5����3��tan��CBD��ֵ��
��������Բ����ʱ��t=5��������Բ�ں�ʱ��t��5����3��tan��CBD��ֵ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��������
��1���ȸ������Ǻ�������ɵ�BC��4���ɹ��ɶ�������AC��3�����֤����ABD����D�������D�����м��ɣ�
��2����������ۣ�������Բ���룬���У��ཻ�����У��ں��Ķ���ɵý��ۣ�
��3������BDEΪֱ��������ʱ����D���߶�AC�Ϻ�����AC������������ٷ֡�BDE��90���͡�DBE��90���ֱ�ͼ���������������ƺ����Ǻ����б���ʽ�ɽ�����⣮
��1���ڡ�ABC�У�
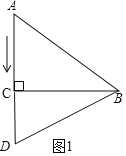
�ߡ�ACB=90����AB=5��![]() ��
��
��![]() ��
��
��BC=ABcos��ABC=5![]() 4��
4��
��![]() ��
��
��AD=AB=5ʱ����ABD=��D��
��CD=AD��AC=5��3=2��
��Rt��BCD��![]() ��
��
��tan��ABD=tan��D=2��
��2����ͼ2����A������E����Բ���У�
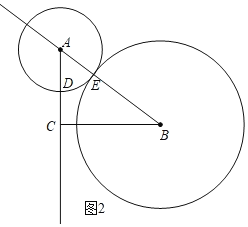
������ã�AD=t��BE=2t��
��t+2t=5��
��ã�t![]() ��
��
������Բ����ʱ���������5��3t����ã�![]() ��
��
������Բ����ʱ����ͼ2��![]() ��
��
������Բ�ཻʱ���������t��5��3t����ã�![]() ��
��
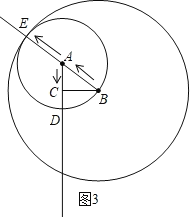
������Բ����ʱ����ͼ3���������2t��t=5����ã�t=5��
������Բ�ں�ʱ���������0��5��t����ã�t��5��
��3������D���߶�AC�ϣ��ҡ�BED=90��ʱ����ͼ4��
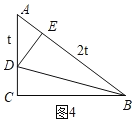
��cosA![]() ����
����![]() ��
��
��ã�![]() ��
��
��CD=3![]() ��
��
��![]() ��
��
����D���߶�AC�ϣ��ҡ�BDE=90������ͼ5����E��EF��BC����AC��F��
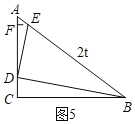
��AE=5��2t��
��EF��BC��
���AEF�ס�ABC��
��![]() ����
����![]() ��
��
��AF=3![]() t��EF=4
t��EF=4![]() t��
t��
��AD=t��
��CD=3��t��DF=AD��AF=t��(3![]() t)
t)![]() t��3��
t��3��
�ߡ�BDE=��EDF+��CDB=��CDB+��CBD=90����
���EDF=��CBD��
�ߡ�EFD=��C=90����
���EFD�ס�DCB��
��![]() ����
����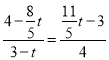 ��
��
��4(4![]() t)=(3��t)(
t)=(3��t)(![]() t��3)��
t��3)��
��ã�t1=5(��)��![]() ��
��
��tan��CBD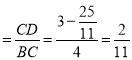 ��
��
����D���߶�AC���ӳ����ϣ��ҡ�BDE=90��ʱ����ͼ6����E��EF��AC����CA���ӳ�����F��
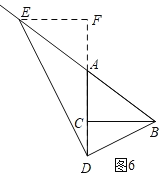
��EF��BC��
���AEF�ס�ABC��
��![]() ����
����![]() ��
��
��AF![]() t��3��EF
t��3��EF![]() t��4��
t��4��
��AD=t��
��CD=t��3��DF=AD+AF=t+(![]() t��3)
t��3)![]() t��3��
t��3��
ͬ���á�EFD�ס�DCB��
��![]() ����
����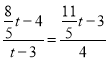 ��
��
��4(![]() t��4)=(t��3)(
t��4)=(t��3)(![]() t��3)��
t��3)��
��ã�t1=5��![]() (��)��
(��)��
��tan��CBD![]() ��
��
����D���߶�AC���ӳ����ϣ��ҡ�DBE=90��ʱ����ͼ7��
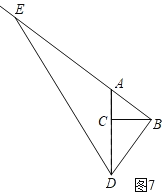
�ߡ�ABC+��CBD=��CBD+��CDB��
���ABC=��CDB��
��tan��ABC=tan��CDB![]() ����
����![]() ��
��
��ã�![]() ��
��
��tan��CBD![]() ��
��
���ϣ�tan��CBD��ֵ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������ABCD �У���E��O��F�ֱ��DZ�AB��AC��AD���е㣬����CE��CF��OE��OF��
��1����֤����BCE�ա�DCF��
��2����AB��BC����ʲô����ʱ���ı���AEOF�����Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
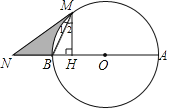
����Ŀ����ͼ��AB�ǡ�O��ֱ����NM���O�����ڵ�M����AB���ӳ��߽��ڵ�N��MH��AB�ڵ�H��
��1����֤����1����2��
��2������N��30����BN��5�����O�İ뾶��
��3���ڣ�2���������£����߶�BN��MN���ӻ�BMΧ�ɵ���Ӱ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ�����ɫ��ͬ�ĺ���ͺ�������һ�������Ĵ�����װ��2�������2������
��1���������һ�����Ǻ���ĸ���Ϊ �����ȴӴ�����ȡ��m�������Żأ����ٴӴ������������һ������������������Ϊ�¼�A�����¼�AΪ��Ȼ�¼�����m�� ��
��2�����Ӵ�����һ���������������б�������״ͼ���г����еȿ��ܽ��������������������ɫ��ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������3��4��4��5��������һ����4�������仯��ͳ������( )
A.ƽ����B.����C.��λ��D.����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
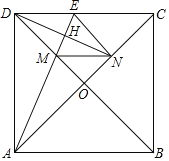
����Ŀ����ͼ����֪��������ABCD�У��Խ���AC��BD���ڵ�O����M���߶�OD�ϣ�����AM���ӳ�����DC�ڵ�E����N���߶�OC�ϣ���ON��OM������DN���߶�AE���ڵ�H������EN��MN��
��1�����EN��BD����֤���ı���DMNE�����Σ�
��2�����EN��DC����֤��AN2��NCAC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻУ�Ļ�������ѧ�����ۺ����ʣ��ٽ���ѧ��ȫ�淢չ��ѧУ��չ�˶������Ż��С��ϲ���������У��ϳ����š��������š��鷨���š��Ƽ����ţ��ֱ�����ĸA��B��C��D���α�ʾ���ĸ����ţ����������ĸ���ĸ�ֱ�д��������ȫ��ͬ�IJ����Ŀ�Ƭ�������ϣ�Ȼ�������ſ�Ƭ���泯��ϴ�Ⱥ���������ϣ�
��1��С�����������ȡһ�ſ�Ƭ����������B�ĸ������� ����
��2��С���ȴ��������ȡһ�ſ�Ƭ����¼�¿�Ƭ�ϵ���ĸ�Żأ��ٴ�ʣ��Ŀ�Ƭ�������ȡһ�ſ�Ƭ����¼�¿�Ƭ�ϵ���ĸ���������б�������״ͼ�����С�����γ�ȡ�Ŀ�Ƭ����һ���ǿƼ�����D�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
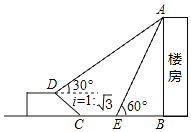
����Ŀ����ͼ����һ���ۺ�ʵ����У�С��Ҫ����һ¥���ĸ߶ȣ���������D�����¥������A������Ϊ30�㣬�����������ߵ��½�C����Ȼ���ڵ�������CB��¥�������������10����E�������¥������A������Ϊ60�㣮��֪����CD��10�ף�ɽ�µ��¶�i��1��![]() ���¶���ָ�����Ǧֱ�߶���ˮƽ���ȵıȣ�����¥��AB�߶ȣ������������ʽ��
���¶���ָ�����Ǧֱ�߶���ˮƽ���ȵıȣ�����¥��AB�߶ȣ������������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ��ֱ�������ε����߳��ֱ�Ϊ![]() �������������ξ���ֱ�������Σ�
�������������ξ���ֱ�������Σ�
��1���ж������������壬���г��ȵ������߶�����ɾ���ֱ�������ε��ǣ���
A��1��2��3 B��1,1,2 C��2,3,4 D��3��4��5��
��2��������֤���κξ���ֱ�������εĽ�Сֱ�DZ���ϴ�ֱ�DZߵı���![]()
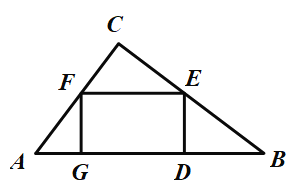
��3��Ӧ����ͼ����һ�����ֱ��������ֽ��![]() �м�һ�����Σ��Ҿ��ε�һ����
�м�һ�����Σ��Ҿ��ε�һ����![]() �ϣ�������������ֱ���
�ϣ�������������ֱ���![]() �ϣ���֪
�ϣ���֪![]() �������������������ֵ��
�������������������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com