
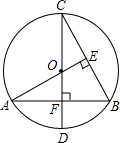
 如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为E,BC=2
如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为E,BC=2| 3 |
 |
| AD |
 |
| BD |
| 1 |
| 2 |
| 1 |
| 2 |
 |
| AD |
 |
| BD |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| CE |
| cos30° |
| ||||
|


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
 某学习小组想了解南京市“迎青奥”健身活动的开展情况,准备采用以下调查方式中的一种进行调查:①从一个社区随机选取200名居民;②从一个城镇的不同住宅楼中随机选取200名居民;③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象.
某学习小组想了解南京市“迎青奥”健身活动的开展情况,准备采用以下调查方式中的一种进行调查:①从一个社区随机选取200名居民;②从一个城镇的不同住宅楼中随机选取200名居民;③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象.. |
| x |
| x1+x2+…+xn |
| n |
. |
| x |
| 1+2+3+4 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=
如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
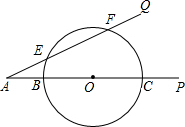 已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:查看答案和解析>>
科目:初中数学 来源: 题型:
 某商店第一次用600元购进某种型号的铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价比第一次贵1元,所以购进数量比第一次少了30支.
某商店第一次用600元购进某种型号的铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价比第一次贵1元,所以购进数量比第一次少了30支.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com