
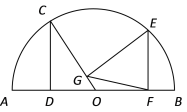
【题目】如图,O是半圆的圆心,半径为4.C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.若∠COA=60°,则FG=______.
科目:初中数学 来源: 题型:
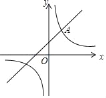
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于点A(﹣3,2),B(n,﹣6)两点.
的图象交于点A(﹣3,2),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积;
(3)请直接写出y1<y2时x的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数y=![]() 的图象与直线y=x+1交于点A(1,a).
的图象与直线y=x+1交于点A(1,a).
(1)求a,k的值;
(2)连结OA,点P是函数y=![]() 上一点,且满足OP=OA,直接写出点P的坐标(点A除外).
上一点,且满足OP=OA,直接写出点P的坐标(点A除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
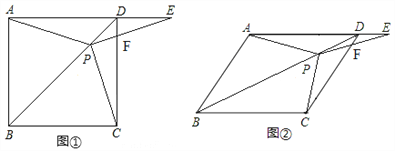
【题目】如图①,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PE=PA,PE交CD于F.
(1)求证: PC=PE;
(2)求∠CPE的度数;
(3)如图②,把正方形ABCD改为菱形ABCD,其它条件不变,若∠ABC=65°,则∠CPE=________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣6,0)、B(2,0)、C(0,6)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足为点E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)过点P(﹣3,m)作x轴的垂线,垂足为点F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P,求出P的坐标.(直接写出结果)
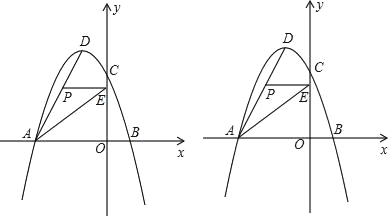
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的2000名学生中作了抽样调查.请根据下面两个不完整的统计图回答以下问题:
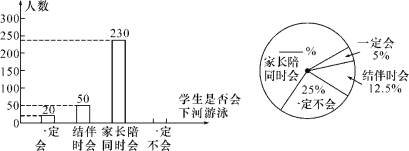
(1)这次抽样调查中,共调查了__ __名学生;
(2)补全两个统计图;
(3)根据抽样调查的结果,估算该校2000名学生中大约有多少人“一定会下河游泳”?
查看答案和解析>>
科目:初中数学 来源: 题型:
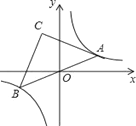
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
A. y=﹣![]() x B. y=﹣
x B. y=﹣![]() x C. y=﹣
x C. y=﹣![]() D. y=﹣
D. y=﹣![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com