
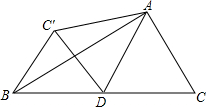
 如图△ABC中,AD为底边上的中线,∠ADC=60°,BC=4,将△ADC沿AD翻折与△ADC′重合,则BC′=2.
如图△ABC中,AD为底边上的中线,∠ADC=60°,BC=4,将△ADC沿AD翻折与△ADC′重合,则BC′=2. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明平时爱动脑筋,深受老师喜爱,今天是小明的生日,老师想考小明,特地准备了一个三角形大蛋糕作为礼物,让小明只切三刀,把大蛋糕分成六等份,小明刚学完有关三角形中线的知识,动了一下脑筋,就把问题解决了,你知道小明如何解决的吗?
小明平时爱动脑筋,深受老师喜爱,今天是小明的生日,老师想考小明,特地准备了一个三角形大蛋糕作为礼物,让小明只切三刀,把大蛋糕分成六等份,小明刚学完有关三角形中线的知识,动了一下脑筋,就把问题解决了,你知道小明如何解决的吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
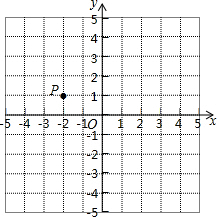 已知P(-2,1).(第(1)(2)要求保留必要的作图轨迹和简单的说理)
已知P(-2,1).(第(1)(2)要求保留必要的作图轨迹和简单的说理) 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
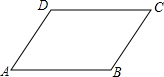 已知?ABCD(如图),将它沿AB方向平移,平移的距离为$\frac{1}{2}$AB.
已知?ABCD(如图),将它沿AB方向平移,平移的距离为$\frac{1}{2}$AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 长方形 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
| 长度 | 5 | 4 | 3 | 2 | 1 |
| 宽度 | x | x+1 | x+2 | x+3 | x+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com