
【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心![]() 出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:线段
出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:线段![]() 、半圆弧
、半圆弧![]() 、线段
、线段![]() 后,回到出发点,蚂蚁离出发点的距离
后,回到出发点,蚂蚁离出发点的距离![]() (蚂蚁所在位置与
(蚂蚁所在位置与![]() 点之间线段的长度)与时间
点之间线段的长度)与时间![]() 之间的图像如图2所示.
之间的图像如图2所示.
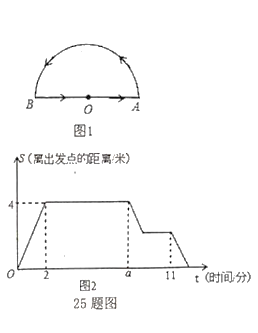
![]() 请直接写出:花坛的半径是____ 米,蚂蚁爬行的速度为____ 米/分;
请直接写出:花坛的半径是____ 米,蚂蚁爬行的速度为____ 米/分;
![]() 计算图中
计算图中![]() 的值;
的值;
![]() 若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了
若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了![]() 分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方离出发点的距离;
②蚂蚁返回点![]() 的时间.(注: 圆周率
的时间.(注: 圆周率![]() 的值取
的值取![]() )
)
【答案】(1)4,2;(2)a=8;(3)①蚂蚁停下来吃食的地方距出发点2米,②蚂蚁返回O的时间为12分钟
【解析】
(1)根据圆上的点到圆心的距离等于半径可知S开始不变时的值即为花坛的半径,然后求出蚂蚁的速度;
(2)根据时间=路程÷速度计算即可求出a;
(3)①根据蚂蚁吃食时离出发点的距离不变判断出蚂蚁在BO段,再求出蚂蚁从B爬到吃食时的时间,然后列式计算即可得解;
②求出蚂蚁吃完食后爬到点O的时间,再加上11计算即可得解.
(1)4,2;
(2)a=(4+4π)÷2=(4+4×3)÷2=8;
(3)∵沿途只有一处食物,
∴蚂蚁只能在BO段吃食物,11﹣8﹣2=1,
∴蚂蚁从B爬1分钟找到食物,4﹣1×2=2(米),
即蚂蚁停下来吃食的地方距出发点2米,
∴2÷2=1(分钟),
∴11+1=12(分钟),
∴蚂蚁返回O的时间为12分钟.


科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象经过点(﹣3,2).
的图象经过点(﹣3,2).
(1)求它的解析式;
(2)在直角坐标中画出该反比例函数的图象;
(3)若﹣3<x<﹣2,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车沿同一平直公路由A地匀速行驶(中途不停留),前往终点B地,甲、乙两车之间的距离S(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.下列说法:
①甲、乙两地相距210千米;②甲速度为60千米/小时;③乙速度为120千米/小时;④乙车共行驶3 ![]() 小时,其中正确的个数为( )
小时,其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按规律填空.
(1)1,3,5,7,9,__________;
(2)2,5,8,11,14,__________;
(3)![]() ,
,![]() ,
,![]() ,
,![]() ,__________;
,__________;
(4)![]() ,
,![]() ,
,![]() ,
,![]() ,__________;
,__________;
(5)2,6,15,31,56,__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明就市电视台的各节目所受欢迎的情况,对本班50名同学进行了一次调查,结果如下:
最受学生欢迎的电视节目
节目 | 人数 |
体育 | 18 |
新闻 | 16 |
综艺 | 8 |
动画 | 5 |
其他 | 3 |
(1)选用适当的统计图描述上表数据;
(2)还能用其他统计图描述吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn﹣1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )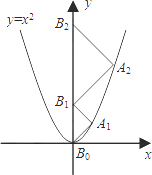
A.2013
B.2014
C.2013 ![]()
D.2014 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查市场上某品牌方便面的色素含量是否符合国家标准,工作人员在超市里随机抽取了某品牌的方便面进行检验.图1和图2是根据调查结果绘制的两幅不完整的统计图,其中A、B、C、D分别代表色素含量为0.05%以下、0.05%~0.1%、0.1%~0.15%、0.15%以上,图1的条形图表示的是抽查的方便面中色素含量分布的袋数,图2的扇形图表示的是抽查的方便面中色素的各种含量占抽查总数的百分比.请解答以下问题:

(1)本次调查一共抽查了多少袋方便面?
(2)将图1中色素含量为B的部分补充完整;
(3)图2中的色素含量为D的方便面所占的百分比是多少?
(4)若色素含量超过0.15%即为不合格产品,某超市这种品牌的方便面共有10000袋,那么其中不合格的产品有多少袋?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数 | 54 | 45 | 30 | 24 | 21 | 12 |
人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0),B(0,2![]() )
)
(1)点(k+1,2k﹣5)关于x轴的对称点在第一象限,a为实数k的范围内的最大整数,求A点的坐标及△AOB的面积;
(2)在(1)的条件下如图1,点P是第一象限内的点,且△ABP是以AB为腰的等腰直角三角形,请直接写出P点坐标;
(3)在(1)的条件下,如图2,以AB、OB的作等边△ABC和等边△OBD,连接AD、OC交于E点,连接BE.
①求证:EB平分∠CED;
②M点是y轴上一动点,求AM+CM最小时点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com