
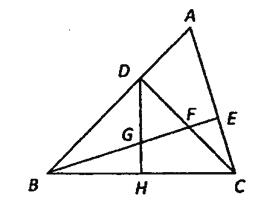
【题目】如图,△ABC中,∠ABC=45![]() ,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G.
,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=![]() BF.
BF.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据三角形的内角和定理求出∠A=∠DFB,推出BD=DC,根据AAS证出△BDF≌△CDA即可;
(2)推出∠AEB=∠CEB,∠ABE=∠CBE,根据ASA证出△AEB≌△CEB,推出AE=CE即可.
(1)证明:∵CD⊥AB,∠ABC=45°,
∴△BCD是等腰直角三角形.
∴BD=CD.
∵∠DBF=90°-∠BFD,∠DCA=90°-∠EFC,且∠BFD=∠EFC,
∴∠DBF=∠DCA.
在Rt△DFB和Rt△DAC中,∠BDF=∠CDA,
∠A=∠DFB,
BD=DC,
∴Rt△DFB≌Rt△DAC(AAS),
∴BF=AC.
(2)证明:在![]() 和
和![]() 中
中
![]() 平分
平分![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() .
.
又由(1),知![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】某校要组建篮球队参加校际比赛,同学们踊跃报名参与选拔,现还有一个名额没有确定,要从甲、乙两位同学中选出一位进入校篮球队,体育老师从身高、个人技术、合作意识、体能四方面对他俩进行了考核评价,每项满分100分.考核结果如下:
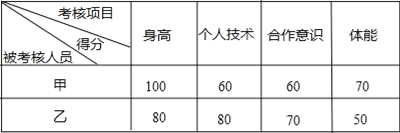
(1)如果根据四项考核项目的平均得分确定人选,那么请你通过计算判断谁将入选校篮球队?
(2)根据校篮球队需要,如果四项考核项目按1:2:2:1的比例确定得分,那么请你通过计算判断谁将入选校篮球队?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各数中,相等的组数有( )
①(﹣5)2与﹣52
②(﹣2)2与22
③(﹣2)3与﹣23
④﹣(﹣3)3与丨﹣33|
⑤﹣(﹣2)2与22 .
A.0组
B.1组
C.2组
D.3组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC中,∠C=90°,E为BC边中点.
(1)尺规作图:以AC边为直径,作⊙O,交AB于点D(保留作图痕迹,标上相应的字母,可不写作法);
(2)连结DE,求证:DE为⊙O的切线;
(3)若AD=4,BD=![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,放有四张质地完全相同的卡片,分别标有数字1,2,3,4.第一次从袋中随机地抽出一张卡片,把其上的数字记为横坐标x,然后把卡片放回袋中,搅匀后第二次再随机地从中抽出一张,把其上的数字记为纵坐标y.
(1)用树状图或列表法把所有可能的点表示出来;
(2)求所得的点在直线y=﹣x+5的点的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com