
【题目】如图,在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
(1)若![]() 的周长为29,
的周长为29,![]() ,求
,求![]() 的长度;
的长度;
(2)若![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)BC=20(2) 20![]()
【解析】
(1)根据三角形的周长可得AD+AF+FD=29,故AD+AF=24.5,根据垂直平分线的性质得到AD=BD,AF=CF,根据BC=BD+CF-DF即可求解;
(2)根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,再根据等边对等角可得∠BAD=∠B,同理可得,∠CAF=∠C,然后利用三角形的内角和定理求出∠B+∠C,再根据![]() =∠BAD+∠CAF ∠BAC代入数据进行计算即可得解.
=∠BAD+∠CAF ∠BAC代入数据进行计算即可得解.
(1)∵![]() 的周长为29,
的周长为29,
∴AD+AF+FD=29,
∵![]()
∴AD+AF=29-4.5=24.5
∵![]() 垂直平分
垂直平分![]() ,
,![]() 垂直平分
垂直平分![]() ,
,
∴AD=BD,AF=CF,
∴BD+CF= AD+AF=24.5
∴BC=BD+CF-DF=24.5-4.5=20
即BC=20;
(2)∵![]() 垂直平分
垂直平分![]() ,
,
∴AD=BD,
∴∠BAD=∠B,
同理可得∠CAF=∠C,
∴![]() =∠BAD+∠CAF ∠BAC=(∠B+∠C)∠BAC,
=∠BAD+∠CAF ∠BAC=(∠B+∠C)∠BAC,
在△ABC中,∠B+∠C=180![]() ∠BAC=100
∠BAC=100![]() ,
,
∴![]() =100
=100![]() 80
80![]() =20
=20![]() .
.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(解决问题)已知![]() ,
,![]() ,
,![]() 是同一平面上的三个点,以线段
是同一平面上的三个点,以线段![]() ,
,![]() 为边,分别作正三角形
为边,分别作正三角形![]() 和正三角形
和正三角形![]() ,连接
,连接![]() ,
,![]() .
.
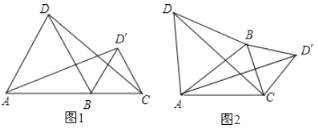
(1)如图1,当点![]() ,
,![]() ,
,![]() 在同一直线上时,线段
在同一直线上时,线段![]() 与
与![]() 的大小关系是__________;
的大小关系是__________;
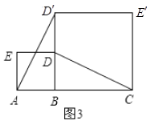
(2)如图2,当![]() ,
,![]() ,
,![]() 为三角形的顶点时(点
为三角形的顶点时(点![]() ,
,![]() ,
,![]() 不在同一条直线上),判断线段
不在同一条直线上),判断线段![]() 与
与![]() 的大小关系是否发生改变,并说明理由;
的大小关系是否发生改变,并说明理由;
(类比猜想)
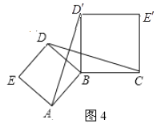
(3)已知![]() ,
,![]() ,
,![]() 是同一平面上的三个点,以线段
是同一平面上的三个点,以线段![]() ,
,![]() 为边,分别作正方形,连接
为边,分别作正方形,连接![]() ,
,![]() ,如图3和图4所示.判断线段
,如图3和图4所示.判断线段![]() 与
与![]() 的大小关系,并在图4(点
的大小关系,并在图4(点![]() ,
,![]() ,
,![]() 不在同一条直线上)中证明你的判断;
不在同一条直线上)中证明你的判断;
(推广应用)(4)上面的这些结论能否推广到任意正多边形(不必证明)?
(5)如图5,![]() 与
与![]() 的大小关系是__________,并写出它们分别在哪两个全等三角形中;
的大小关系是__________,并写出它们分别在哪两个全等三角形中;
(6)请在图6中连接图中两个顶点,构造处一组全等三角形,并写出这两个全等的三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.

(1)求证:四边形DEBF是菱形;
(2)请判断四边形AGBD是什么特殊四边形? 并加以证明;
(3)若AD=1,求四边形AGCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向.求货船的航行速度.(精确到0.1海里/时,参考数据:![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
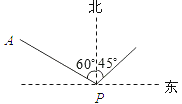
查看答案和解析>>
科目:初中数学 来源: 题型:
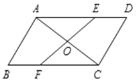
【题目】如图,AC是平行四边形ABCD的一条对角线,过AC中点O的直线分别交 AD,BC 于点 E,F.
(1)求证:四边形AECF是平行四边形;
(2)当 EF 与 AC 满足什么条件时,四边形 AECF 是菱形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com