
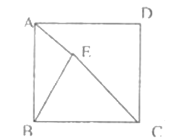
【题目】如图,点![]() 为正方形
为正方形![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,则
,则![]() _________.
_________.
【答案】![]()
【解析】
作EG⊥AB于G,EH⊥BC于H,由四边形ABCD是正方形,得到∠ABC=90°,由四边形BHEG是矩形,得到EG=BH,BG=EH,在Rt△ABE中根据勾股定理可求出AB的长,根据三角形的面积公式得到EG的长,在Rt△BGE中根据勾股定理得到BG的值,再在Rt△CEH中根据勾股定理得到CE的值即可.
作EG⊥AB于G,EH⊥BC于H,
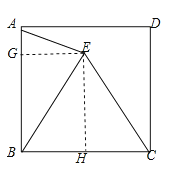
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴四边形BHEG是矩形,∴
EG=BH,BG=EH,
∵∠AEB=90°,若AE=2,BE=3,
∴AB=![]() ,
,
∵S△ABE=![]() ABEG=
ABEG=![]() AEBE,
AEBE,
∴![]() EG=2×3,
EG=2×3,
∴EG=![]() ,
,
∴BG=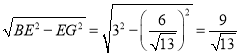 ,
,
∴HE=BG=![]() ,BH=EG=
,BH=EG=![]() ,
,
∴CH=BC-BH=![]() ,
,
∴CE=![]() ,
,
故答案为:![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q.
(1)求∠BPQ的度数;
(2)若PQ=3,EP=1,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张背面看上去无差别的扑克牌,正面分别写着5,6,7,8,9,洗匀后正面向下放在桌子上,从中随机抽取2张,抽出的卡片上的数字恰好是两个连续整数的概率是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在△ABC的边AB上,且AD=CD,

(1)用直尺和圆规作∠BDC的平分线DE,交BC于点E(不写作法,保留作图痕迹);
(2)在(1)的条件下,判断DE与AC的位置关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D是BC边上一动点,点E,F分别在AB,AC边上,连接AD,DE,DF,且∠ADE=∠ADF=60°.
小明通过观察、实验,提出猜想:在点D运动的过程中,始终有AE=AF,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:利用AD是∠EDF的角平分线,构造△ADF的全等三角形,然后通过等腰三角形的相关知识获证.
想法2:利用AD是∠EDF的角平分线,构造角平分线的性质定理的基本图形,然后通过全等三角形的相关知识获证.
想法3:将△ACD绕点A顺时针旋转至△ABG,使得AC和AB重合,然后通过全等三角形的相关知识获证.
请你参考上面的想法,帮助小明证明AE=AF.(一种方法即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为(3,4),
的坐标为(3,4),![]() 轴于点
轴于点![]() ,
,![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,点
,点![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正方向运动,
轴正方向运动,![]() 与直线
与直线![]() 交于
交于![]() ,则
,则![]() 的面积( )
的面积( )
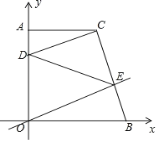
A.逐渐变大B.先变大后变小C.逐渐变小D.始终不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地在城区美化工程招标时,有甲、乙两个工程队投标.经测算,获得以下信息:
信息1:乙队单独完成这项工程需要60天;
信息2:若先由甲、乙两队合做16天,剩下的工程再由乙队单独做20天可以完成;
信息3:甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.
根据以上信息,解答下列问题:
(1)甲队单独完成这项工程需要多少天?
(2)若该工程计划在50天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲、乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在所给坐标系中画出二次函数y=x2+bx+c的图象.
(4)写出当y<0时,x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com