
【题目】阅读材料:善于思考的小军在解方程组![]() 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法:
解:将方程②变形为4x+10y+y=5,即2(2x+5y)+y=5,③
把方程①代入③得2×3+y=5,∴y=-1,
把y=-1代入①得x=4,
∴方程组的解为![]() .
.
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组 ![]()
(2)已知x,y满足方程组![]() 求整式x2+4y2+xy的值;
求整式x2+4y2+xy的值;
【答案】(1)方程组的解为![]() ;(2)19.
;(2)19.
【解析】分析:(1)模仿小军的“整体代换”法,求出方程组的解即可;
(2)方程组整理后,模仿小军的“整体代换”法,求出所求式子的值即可.
详解:(1) 将方程②变形为9x-6y+2y=19,
即3(3x-2y)+2y=19, ③
把方程①代入③得3×5+2y=19,
∴y=2,
把y=2代入①得
x=3,
∴方程组的解为![]()
(2) 由①得3(x2+4y2)=47+2xy,
即x2+4y2=![]() ,③
,③
把方程③代入②得2×![]() +xy=36,
+xy=36,
解得xy=2
∴把xy=2代入③得
x2+4y2=17.
∴x2+4y2+xy=17+2=19.
答:整式x2+4y2+xy的值为19.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)填空:b= ,c= ;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;
(4)如图②,点N的坐标为(﹣![]() ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园艺术节活动中,参加摄影大赛的作品共有98件,比上届参赛作品增加了40%,则上届参赛作品有( )
A.39件B.60件C.70件D.71件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由

∵∠1=∠2 ( )
∠2=∠3 ,∠1=∠4( )
∴∠3=∠4( )
∴_______∥_______ ( )
∴∠C=∠ABD( )
∵∠C=∠D( )
∴∠D=∠ABD( )
∴DF∥AC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】比邻而居的蜗牛神和蚂蚁王相约,第二天上午8时结伴出发,到相距16米的银杏树下参加探讨环境保护问题的微型动物首脑会议.蜗牛神想到“笨鸟先飞”的古训,于是给蚂蚁王留下一纸便条后提前2小时独自先行,蚂蚁王按既定时间出发,结果它们同时到达.已知蚂蚁王的速度是蜗牛神的4倍,求它们各自的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为验证“掷一个质地均匀的骰子,向上的点数为偶数的概率是0.5”,下列模拟实验中,不科学的是( )
A. 袋中装有1个红球一个绿球,它们除颜色外都相同,计算随机摸出红球的概率
B. 用计算器随机地取不大于10的正整数,计算取得奇数的概率
C. 随机掷一枚质地均匀的硬币,计算正面朝上的概率
D. 如图,将一个可以自由旋转的转盘分成甲、乙、丙3个相同的扇形,转动转盘任其自由停止,计算指针指向甲的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
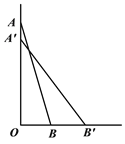
【题目】如图,一架2.5米长的梯子斜立在竖直的墙上,此时梯足B距底端O为0.7米。(1)求OA的长度。(2)如果梯子顶端下滑0.4米,则梯子将滑出多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:
(x-1)(x+1)=x2-1, (x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1, (x-1)(x4+x3+x2+x+1)=x5-1,
……
(1)试写出第五个等式;
(2)试求26+25+24+23+22+2+1的值;
(3)判断22 017+22 016+22 015+…+22+2+1的值的个位数字是几.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com