练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正方形ABFG和正方形CDEF中，使点B、C的坐标分别为（0，0）和（4，0）．

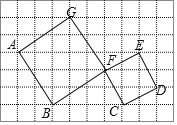
    （1）在图中建立平面直角坐标系；

    （2）写出A点的坐标；

    （3）画出正方形EFCD左平移2个单位，上平移1个单位后的正方形E′F′C′D′．

    【答案】（1）平面直角坐标系如图所示，见解析；（2）A（﹣2，3）；（3）如图所示，正方形E′F′C′D′即为所求．见解析．

    【解析】

    （1）根据点B、C的坐标分别为（0，0）和（4，0），即可得到直角坐标系；
    （2）根据A点的位置，即可得到其坐标；
    （3）根据正方形EFCD左平移2个单位，上平移1个单位，即可得到正方形E′F′C′D′．

    解：（1）平面直角坐标系如图所示，

    （2）由图可得，A（﹣2，3）；

    （3）如图所示，正方形E′F′C′D′即为所求．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】鸡兔同笼问题是我国古代著名趣题之一，大约在 1500 年前，《孙子算经》中就记载了这个有趣的问题．书中是这样叙述的：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”这四句话的意思是：有若干只鸡、兔同在一个笼子里，从上上面数，有 35 个头；从下面数，有 94 只脚 ．求笼中各有几只鸡和兔？经计算可得（ ）

    A. 鸡 20 只，兔 15 只 B. 鸡 12 只，兔 23 只

    C. 鸡 15 只，兔 20 只 D. 鸡 23 只，兔 12 只

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图在平面直角坐标系中，△ABC各顶点的坐标分别为：A（4，0），B（﹣1，4），C（﹣3，1）

    （1）在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称；

    （2）写出点A′B′C′的坐标；

    （3）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y＝x＋b与抛物线y＝x2＋x＋c相交于点A（6，8）与点B，P是线段AB的中点，D是抛物线上的一个动点，直线DP交x轴于点C．

    （1）分别求出这两个函数的关系式，并写出点B，P的坐标．

    （2）四边形ACBD能否成为平行四边形？若能，请求出线段OC的长度；若不能，请说明理由．

    （3）当点D的坐标为（4，2）时，△APD是什么特殊三角形？请说明理由，并写出所有符合这一特殊性的点D的坐标．

    　　　　

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】早晨，小明步行到离家900米的学校去上学，到学校时发现眼镜忘在家中，于是他立即按原路步行回家，拿到眼镜后立即按原路骑自行车返回学校．已知小明步行从学校到家所用的时间比他骑自行车从家到学校所用的时间多10分钟，小明骑自行车速度是步行速度的3倍．

    （1）求小明步行速度（单位：米/分）是多少；

    （2）下午放学后，小明骑自行车回到家，然后步行去图书馆，如果小明骑自行车和步行的速度不变，小明步行从家到图书馆的时间不超过骑自行车从学校到家时间的2倍，那么小明家与图书馆之间的路程最多是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，CF⊥AB，垂足为F，M为BC的中点，E为AC上一点，且ME＝MF．若∠A＝50°，则∠FME的度数为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

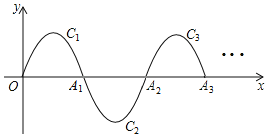
    【题目】如图，一段抛物线：，记为，它与x轴交于点O，；将绕点旋转得，交x轴于点；将绕点旋转得，交x轴于点；如此进行下去，得到一“波浪线”，若点在此“波浪线”上，则m的值为　　

    A. 4 B. C. D. 6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．

    种类

    A

    B

    C

    D

    E

    出行方式

    共享单车

    步行

    公交车

    的士

    私家车

    根据以上信息，回答下列问题：

    （1）参与本次问卷调查的市民共有 人，其中选择B类的人数有 人；

    （2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；

    （3）该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知两条射线OM∥CN，动线段AB的两个端点A、B分别在射线OM、CN上，且∠C=∠OAB=108°，F在线段CB上，OB平分∠AOF，OE平分∠COF．

    （1）请在图中找出与∠AOC相等的角，并说明理由；

    （2）若平行移动AB，那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化？若变化，找出变化规律；若不变，求出这个比值；

    （3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=2∠OBA？若存在，请求出∠OBA度数；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案