
【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=![]() 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
(3)当常数k满足![]() ≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
【答案】(1)m的值为﹣1,n的值为1.(2)y=2(x+1)2﹣6或y=﹣![]() (x﹣3)2+2.(3)
(x﹣3)2+2.(3)![]() ≤S≤
≤S≤![]() .
.
【解析】
试题分析:(1)确定直线y=mx+1与y轴的交点坐标,将其代入抛物线解析式中即可求出n的值;再根据抛物线的解析式找出顶点坐标,将其代入直线解析式中即可得出结论;(2)确定直线与反比例函数图象的交点坐标,由此设出抛物线的解析式,再由直线的解析式找出直线与x轴的交点坐标,将其代入抛物线解析式中即可得出结论;(3)由抛物线解析式找出抛物线与y轴的交点坐标,再根据抛物线的解析式找出其顶点坐标,由两点坐标结合待定系数法即可得出与该抛物线对应的“带线”l的解析式,找出该直线与x、y轴的交点坐标,结合三角形的面积找出面积S关于k的关系上,由二次函数的性质即可得出结论.
试题解析:(1)令直线y=mx+1中x=0,则y=1,
即直线与y轴的交点为(0,1);
将(0,1)代入抛物线y=x2﹣2x+n中,
得n=1.
∵抛物线的解析式为y=x2﹣2x+1=(x﹣1)2,
∴抛物线的顶点坐标为(1,0).
将点(1,0)代入到直线y=mx+1中,
得:0=m+1,解得:m=﹣1.
答:m的值为﹣1,n的值为1.
(2)将y=2x﹣4代入到y=![]() 中有,
中有,
2x﹣4=![]() ,即2x2﹣4x﹣6=0,
,即2x2﹣4x﹣6=0,
解得:x1=﹣1,x2=3.
∴该“路线”L的顶点坐标为(﹣1,﹣6)或(3,2).
令“带线”l:y=2x﹣4中x=0,则y=﹣4,
∴“路线”L的图象过点(0,﹣4).
设该“路线”L的解析式为y=m(x+1)2﹣6或y=n(x﹣3)2+2,
由题意得:﹣4=m(0+1)2﹣6或﹣4=n(0﹣3)2+2,
解得:m=2,n=﹣![]() .
.
∴此“路线”L的解析式为y=2(x+1)2﹣6或y=﹣![]() (x﹣3)2+2.
(x﹣3)2+2.
(3)令抛物线L:y=ax2+(3k2﹣2k+1)x+k中x=0,则y=k,
即该抛物线与y轴的交点为(0,k).
抛物线L:y=ax2+(3k2﹣2k+1)x+k的顶点坐标为(﹣![]() ,
,![]() ),
),
设“带线”l的解析式为y=px+k,
∵点(﹣![]() ,
,![]() )在y=px+k上,
)在y=px+k上,
∴![]() =﹣p
=﹣p![]() +k,
+k,
解得:p=![]() .
.
∴“带线”l的解析式为y=![]() x+k.
x+k.
令∴“带线”l:y=![]() x+k中y=0,则0=
x+k中y=0,则0=![]() x+k,
x+k,
解得:x=﹣![]() .
.
即“带线”l与x轴的交点为(﹣![]() ,0),与y轴的交点为(0,k).
,0),与y轴的交点为(0,k).
∴“带线”l与x轴,y轴所围成的三角形面积S=![]() |﹣
|﹣![]() |×|k|,
|×|k|,
∵![]() ≤k≤2,
≤k≤2,
∴![]() ≤
≤![]() ≤2,
≤2,
∴S=![]() =
= =
=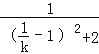 ,
,
当![]() =1时,S有最大值,最大值为
=1时,S有最大值,最大值为![]() ;
;
当![]() =2时,S有最小值,最小值为
=2时,S有最小值,最小值为![]() .
.
故抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围为![]() ≤S≤
≤S≤![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1056张照片,如果全班有x名同学,根据题意,列出方程为( )
A.x(x+1)=1056B.x(x-1)=1056C.x(x+1)=1056×2D.x(x-1)=1056×2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
|
| 0 | 1 | 2 | 3 | 4 | … |
| … | 3 |
|
|
| 0 |
| 0 |
| 3 | … |
其中,![]() =____________.
=____________.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分.
(3)观察函数图像,写出两条函数的性质:

(4)进一步探究函数图像发现:
①函数图像与![]() 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程![]() 有___________个实数根;
有___________个实数根;
②方程![]() 有___________个实数根;
有___________个实数根;
③关于![]() 的方程
的方程![]() 有4个实数根,
有4个实数根,![]() 的取值范围是_______________________
的取值范围是_______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的数学作业本的纸上都是等距离的横线,他在上面任意画一条不与这些横线平行的直线,那么这条直线被这些横线所截得的线段( )
A. 平行 B. 相等 C. 平行或相等 D. 不相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次有24000名学生参加的数学质量抽测的成绩中,随机取2000名考生的数学成绩进行分析,则在该抽样中,样本指的是( ).
A.所抽取的2000名考生的数学成绩
B.24000名考生的数学成绩
C.2000
D.2000名考生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到100个小三角形,则需要操作的次数是( )
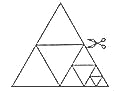
A.25 B.33 C.34 D.50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com