
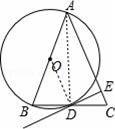
如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交底边BC于D.
(1)求证:BD=CD;
(2)若AB=3,cos∠ABC=
 ,在腰AC上取一点E使AE=
,在腰AC上取一点E使AE=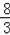
 ,试判断DE与⊙O的位置关系,并证明.
,试判断DE与⊙O的位置关系,并证明.
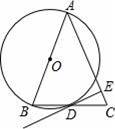

【考点】切线的判定;等腰三角形的性质;圆周角定理.
【专题】证明题.
【分析】(1)连结AD,如图,根据圆周角角定理,由AB为直径得∠ADB=90°,然后根据等腰三角形的性质可得BD=CD;
(2)连结OD,如图,在Rt△ABD中,先利用余弦定义计算出BD=
 AB=1,则Cd=1,再利用勾股定理计算出AD=2
AB=1,则Cd=1,再利用勾股定理计算出AD=2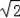
 ,则有
,则有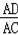

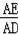
 =
=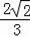
 ,加上∠DAE=∠CAD,于是可判断△ADE∽△ACD,所以∠AED=∠ADC=90°,接着证明OD为△ABC的中位线得到OD∥AC,所以OD⊥DE,则根据切线的判定定理可判断DE为⊙O的切线.
,加上∠DAE=∠CAD,于是可判断△ADE∽△ACD,所以∠AED=∠ADC=90°,接着证明OD为△ABC的中位线得到OD∥AC,所以OD⊥DE,则根据切线的判定定理可判断DE为⊙O的切线.
【解答】(1)证明:连结AD,如图,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
而AB=AC,
∴BD=CD;
(2)解:DE与⊙O相切.理由如下:
连结OD,如图,
在Rt△ABD中,∵cos∠ABD=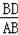
 =
=
 ,
,
∴BD=
 AB=
AB=
 ×3=1,
×3=1,
∴AD=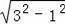
 =2
=2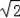
 ,CD=1,
,CD=1,
∵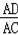
 =
=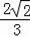
 ,
,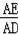
 =
=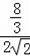
 =
=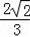
 ,
,
∴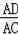
 =
=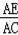
 ,
,
而∠DAE=∠CAD,
∴△ADE∽△ACD,
∴∠AED=∠ADC=90°,
∴DE⊥AC,
∵OA=OB,BD=CD,
∴OD为△ABC的中位线,
∴OD∥AC,
∴OD⊥DE,
∴DE为⊙O的切线.

【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了圆周角定理和等腰三角形的性质.


科目:初中数学 来源: 题型:
下列说法中,正确的是( )
A.“打开电视,正在播放河南新闻节目”是必然事件
B.某种彩票中奖概率为10%是指买十张一定有一张中奖
C.神舟飞船发射前需要对零部件进行抽样调查
D.了解某种节能灯的使用寿命适合抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
用长为32米的篱笆围一个矩形养鸡场.设围成的矩形一边长为x米.
(1)当x为何值时,围成的养鸡场面积为60平方米;
(2)请问能否围成面积为70平方米的养鸡场?如果能,请求出其边长;如果不能,请说明
理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,则下列关系不正确的是( )
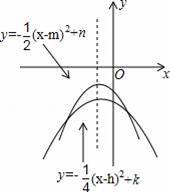

A.k=n B.h=m C.k<n D.h<0,k<0
查看答案和解析>>
科目:初中数学 来源: 题型:
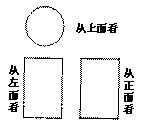
)如图是某种几何体的三视图,这个几何体是_________;
若从正面看时,长方形的宽为10m,高为20m,试求此几何体的表面积是多少m2 ?(结果用π表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com