
在平面直角坐标系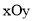 中,二次函数
中,二次函数 的图像与
的图像与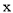 轴交于点A,B(点B在点A的左侧),与
轴交于点A,B(点B在点A的左侧),与 轴交于点C,过动点H(0,
轴交于点C,过动点H(0,  )作平行于
)作平行于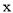 轴的直线,直线与二次函数
轴的直线,直线与二次函数 的图像相交于点D,E.
的图像相交于点D,E.
(1)写出点A,点B的坐标;
(2)若 ,以DE为直径作⊙Q,当⊙Q与
,以DE为直径作⊙Q,当⊙Q与 轴相切时,求
轴相切时,求 的值;
的值;
(3)直线上是否存在一点F,使得△ACF是等腰直角三角形?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

(1)(4,0)和(-1,0);(2) ;(3)存在,m=
;(3)存在,m=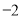 或
或 或3或
或3或 .
.
【解析】
试题分析:(1)A、B两点的纵坐标都为0,所以代入y=0,求解即可.
(2)由圆和抛物线性质易得圆心Q位于直线与抛物线对称轴的交点处,则Q的横坐标为 ,可推出D、E两点的坐标分别为:
,可推出D、E两点的坐标分别为: ,因为D、E都在抛物线上,代入一点即可得m.
,因为D、E都在抛物线上,代入一点即可得m.
(3)使得△ACF是等腰直角三角形,重点的需要明白有几种情形,分别以三边为等腰三角形的两腰或者底,则共有3种情形;而三种情形中F点在AC的左下或右上方又各存在2种情形,故共有6种情形.求解时.利用全等三角形知识易得m的值.
试题解析:【解析】
(1)当y=0时,有 ,解之得:
,解之得: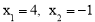 ,
,
∴A、B两点的坐标分别为(4,0)和(-1,0).
(2)∵⊙Q与 轴相切,且与
轴相切,且与 交于D、E两点,
交于D、E两点,
∴圆心O位于直线与抛物线对称轴的交点处,且⊙Q的半径为H点的纵坐标 (
( ).
).
∵抛物线的对称轴为 ,
,
∴D、E两点的坐标分别为: 且均在二次函数
且均在二次函数 的图像上.
的图像上.
∵ ,解得
,解得 或
或 (不合题意,舍去).
(不合题意,舍去).
(3)存在.
①当∠ACF=90°,AC=FC时,如答图1,
过点F作FG⊥y轴于G,∴∠AOC=∠CGF=90°.
∵∠ACO+∠FCG=90°,∠GFC+∠FCG=90°,∴∠ACO=∠CFG.
∴△ACO≌△∠CFG,∴CG=AO=4.
∵CO=2,
∴ 或
或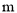 =OG=2+4=6.
=OG=2+4=6.
②当∠CAF=90°,AC=AF时,如答图2,
过点F作FP⊥x轴于P,∴∠AOC=∠APF=90°.
∵∠ACO+∠OAC=90°,∠FAP+∠OAC=90°,∴∠ACO=∠FAP.
∴△ACO≌△∠FAP,∴FP =AO=4.
∴ 或
或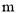 =FP =4.
=FP =4.

③当∠AFC=90°,FA=FC时,如答图3,
则F点一定在AC的中垂线上,此时存在两个点分别记为F,F′,
分别过F,F′两点作x轴、y轴的垂线,分别交于E,G,D,H.
∵∠DFC+∠CFE=∠CFE+∠EFA=90°,∴∠DFC=∠EFA.
∵∠CDF=∠AEF,CF=AF,∴△CDF≌△AEF.
∴CD=AE,DF=EF.∴四边形OEFD为正方形.
∴OA=OE+AE=OD+AE=OC+CD+AE=OC+2CD.
∴4=2+2•CD.∴CD=1,∴m=OC+CD=2+1=3.
∵∠HF′C+∠CGF′=∠CGF′+∠GF′A,∴∠HF′C=∠GF′A.
∵∠HF′C=∠GF′A,CF′=AF′.∴△HF′C≌△GF′A.∴HF′=GF′,CH=AG.
∴四边形OHF′G为正方形.
∴ .∴OH=1.
.∴OH=1.
∴m=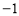 .
.
∵ ,∴y的最大值为
,∴y的最大值为 .
.
∵直线l与抛物线有两个交点,∴m< ∴m可取值为m=
∴m可取值为m=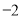 或
或 或3或
或3或 .
.
综上所述,m的值为m=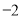 或
或 或3或
或3或 .
.

考点:1.二次函数综合题; 2.单动点问题;3.等腰直角三角形存在性问题;4.二次函数的性质;5.曲线上点的坐标与方程的关系;6.直线与圆的位置关系;7.全等三角形的判定和性质;8.正方形的判定和性质;9.分类思想的应用.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源:2014年初中毕业升学考试(江苏徐州卷)数学(解析版) 题型:解答题
如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG.
(1)试说明四边形EFCG是矩形;
(2)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中,
①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
②求点G移动路线的长.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:解答题
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC﹣CD﹣DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),
△PAB面积为S(cm2).
(1)当t=2时,求S的值;
(2)当点P在边DA上运动时,求S关于t的函数表达式;
(3)当S=12时,求t的值.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:填空题
2014年南京青奥会某项目6名礼仪小姐身高如下(单位:cm):168,166,168,167,169,168,则他们身高的众数是 cm,极差是 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com