
【题目】已知四边形ABCD和AEFG都是正方形,
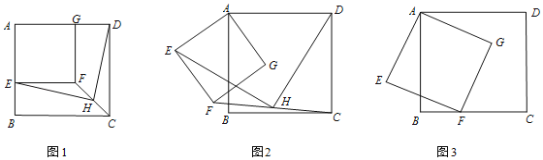
(1)如图1,E、G分别在AB、AD上,连CF,H为CF的中点,EH与DH的位置关系是 ,数量关系是 .
(2)如图2,在图1的基础上,把正方形AEFG绕A点顺时针旋转α(α为锐角),(1)中结论是否仍成立?若成立,请证明;若不成立,请说明理由.
(3)如图3,在(2)旋转过程中,当点F落在BC上,且AE:AB= 时,有AB平分EF.
【答案】(1)DH⊥EH,DH=EH;(2)结论:DH⊥EN,DH=EH=HN.理由见解析;(3)AE:AB=![]() :3.
:3.
【解析】
(1)如图1中,延长EH到N,使得HN=EH.连接DN,CN.只要证明△ADE≌△CDN(SAS),推出DE=DN,∠ADE=∠CDN,∠EDN=∠ADC=90°再利用等腰直角三角形的性质即可解决问题;
(2)结论:DH⊥EN,DH=EH=HN.如图2中,延长EH到N,使得HN=EH.连接DN,CN,DE,延长NC交AD于点M.想办法证明△ADE≌△CDN(SAS)即可解决问题;
(3)如图3中,作EN⊥AB于N设BF交AB于M.设BM=NM=a,想办法求出AE,AB(用a表示),即可解决问题;
解:(1)如图1中,延长EH到N,使得HN=EH.连接DN,CN,DE.
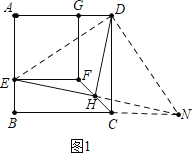
∵FH=HC,∠FHE=∠CHN,EH=HN,
∴△FHE≌△CHN(SAS),
∴EF=CN,∠FEH=∠CNH,
∴EF∥CN,
∵四边形ABCD和AEFG都是正方形,
∴AD=DC,∠DAE=∠ADC=∠AEF=90°,AE=EF=CN,
∴EF⊥AB,∵AB∥CD,
∴EF⊥CD,∵EF∥CN,
∴CN⊥CD,
∴∠DCN=∠DAE=90°
∵AD=CD,AE=CN,
∴△ADE≌△CDN(SAS),
∴DE=DN,∠ADE=∠CDN,
∴∠EDN=∠ADC=90°,
∵EH=HN,
∴DH⊥EN,DH=EH=HN,
故答案为:DH⊥EH,DH=EH.
(2)结论:DH⊥EN,DH=EH=HN.
理由:如图2中,延长EH到N,使得HN=EH.连接DN,CN,DE,延长NC交AD于点M.
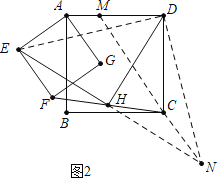
∵FH=HC,∠FHE=∠CHN,EH=HN,
∴△FHE≌△CHN(SAS),
∴EF=CN,∠FEH=∠CNH,
∴EF∥CN,
∵四边形ABCD和AEFG都是正方形,
∴AD=DC,∠DAE=∠ADC=90°,AE=EF=CN,EF∥AG,
∵EF∥AG,EF∥NM,
∴AG∥NM,
∴∠GAD=∠NMD,
∵∠EAD=90°+∠DAG,∠DCN=90°+∠DMC,
∴∠EAD=∠DCN,
∵AD=CD,AE=CN,
∴△ADE≌△CDN(SAS),
∴DE=DN,∠ADE=∠CDN,
∴∠EDN=∠ADC=90°,
∵EH=HN,
∴DH⊥EN,DH=EH=HN.
(3)如图3中,作EN⊥AB于N设BF交AB于M.
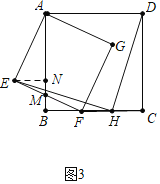
∵∠ENM=∠B=90°,∠EMN=∠BMF,EM=MF,
∴△ENM≌FBM(AAS),
∴NM=BM,设BM=NM=a,
∵AE=2EM,
∴tan∠EAM=![]() =
=![]()
∵∠NEM+∠AEN=90°,∠EAN+∠AEN=90°,
∴∠EAN=∠NEM,
∴tan∠EAN=tan∠NEM=![]() ,
,
∴EN=2a,AN=4a,
∴AB=6a,AE=![]() =
=![]() ,
,
∴AE:AB=![]() :6a=
:6a=![]() :3.
:3.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
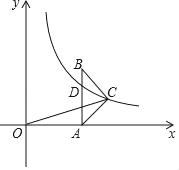
【题目】如图,在△ABC中,AC=BC,AB⊥x轴于A,反比例函数y=![]() (x>0)的图象经过点C,交AB于点D,已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D,已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值.
(2)连接OC,若AD=AC,求CO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()
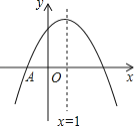
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量 | 房间价格 | 总维护费用 | |
提价前 | 60 | 200 | 60×20 |
提价后 |
|
|
|
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+4ax+c的最大值为4,且图象过点(﹣3,0).
(1)求二次函数解析式;
(2)若将该二次函数的图象绕着原点旋转180°,请直接写出旋转后图象的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
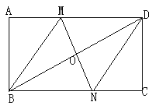
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙I是△ABC的内切圆,切点分别是D、E、F.
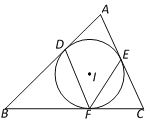
(1)若∠B=50°,∠C=70°,则∠DFE的度数为 ;
(2)若∠DFE=50°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+bx+c,函数值y与自变量x之间的部分对应值如下表:
x | … | ﹣4 | ﹣1 | 0 | 1 | … |
y | … | ﹣2 | ﹣1 | ﹣2 | ﹣7 | … |
(1)此二次函数图象的对称轴是直线,此函数图象与x轴交点个数为 .
(2)求二次函数的函数表达式;
(3)当﹣5<x<﹣1时,请直接写出函数值y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com