
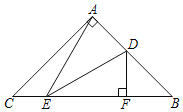
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D、点E分别在AB、BC边上,若∠BED+![]() ∠AED=45°,过点D作DF⊥BC,垂足为F,若BC=3
∠AED=45°,过点D作DF⊥BC,垂足为F,若BC=3![]() ,则EF=_____.
,则EF=_____.
【答案】![]()
【解析】
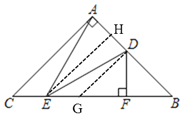
如图中,作EH⊥AB于H,DG⊥AB交BC于点G.只要证明AE=DE,BF=FG,GE=EC即可解决问题.
解:如图中,作EH⊥AB于H,DG⊥AB交BC于点G.
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
∵EH⊥AB,
∴∠EHB=90°,
∴∠BEH=45°,
∴∠BED+∠DEH=45°,
∵2∠BED+∠AED=90°,
∴∠BED+∠AEH=45°,
∴∠DEH=∠AEH,
∵∠EDH+∠DEH=90°,∠EAH+∠HEA=90°,
∴∠EDH=∠EAH,
∴ED=EA.
∵∠B=45°,∠BDG=90°,
∴∠B=∠BGD=45°,
∴DB=DG,
∵DF⊥BG,
∴BF=FG,
∵ED=EA,EH⊥AD,
∴DH=HA,
∵DG∥EH∥AC,
∴EG=EC,
∴EF=FG+GE=![]() BG+
BG+![]() CG=
CG=![]() BC=
BC=![]() .
.
答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
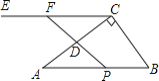
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,
中点,![]() ,动点
,动点![]() 以每秒1个单位长的速度从点
以每秒1个单位长的速度从点![]() 出发向点
出发向点![]() 移动,连接
移动,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,设点
,设点![]() 移动时间为
移动时间为![]() 秒.
秒.
(1)求![]() 与
与![]() 间的距离;
间的距离;
(2)![]() 为何值时,四边形
为何值时,四边形![]() 为平行四边形;
为平行四边形;
(3)当PF=4时,求t的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
为了考察甲、乙两种成熟期小麦的株高长势状况,现从中各随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 | 63 | 66 | 63 | 61 | 64 | 61 |
乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(2)现将进行两种小麦优良品种杂交试验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况.请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座石拱桥的桥拱是以![]() 为圆心,
为圆心,![]() 为半径的一段圆弧.
为半径的一段圆弧.

![]() 请你确定弧
请你确定弧![]() 的中点;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
的中点;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
![]() 如果已知石拱桥的桥拱的跨度(即弧所对的弦长)为
如果已知石拱桥的桥拱的跨度(即弧所对的弦长)为![]() 米,拱高(即弧的中点到弦的距离)为
米,拱高(即弧的中点到弦的距离)为![]() 米,求桥拱所在圆的半径.
米,求桥拱所在圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象与x轴的两个交点A,B关于直线x=﹣1对称,且AB=6,顶点在函数y=2x的图象上,则这个二次函数的表达式为________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
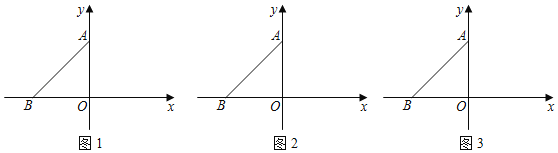
【题目】如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(0,4),点B在x的负半轴上,△AOB的面积为8,作△AOB关于y轴的对称图形,点B的对应点为C.
(1)求线段OC的长;
(2)点D从A点出发,沿线段AO向终点O运动,同时点E从点C出发,沿x轴的正方向运动,且CE=AD,连接DE交AC于点G,判断DG和EG的数量关系,并说明理由.
(3)在(2)的条件下,当∠CEG=∠ABD时,求点G点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了调查学生对课改实验的满意度,随机抽取了部分学生作问卷调查:用“A”表示“很满意“,“B”表示“满意”,“C”表示“比较满意”,“D”表示“不满意”.工作人员根据问卷调查数据绘制了两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
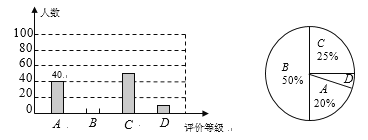
(1)本次问卷调查,共调查了多少名学生?
(2)将条形统计图中的B等级补完整;
(3)求出扇形统计图中,D等级所对应扇形的圆心角度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com