Question

7．如图1，抛物线的顶点D在y轴上，与x轴交于A，B两点，我们把抛物线上A，B两点之间的部分与$\widehat{AB}$所围成的封闭图形称为“锅线”，顶点D称为“锅底”，点D到线段AB的距离称为“锅深”上面的$\widehat{AB}$称为“锅盖”，$\widehat{AB}$的中点C到线段AB的距离称为“锅盖高”，若△ADB为等腰三角形，则此“锅线”称为“标准锅线”．
（1）若图1中的“锅线”为“标准锅线”，“锅盖高”为1dm，“锅深”为3dm，求抛物线的解析式及$\widehat{AB}$所在圆的圆心坐标；
（2）在（1）的情况下，如图2，若点E（-2，n）是“标准锅线”中抛物线上的一点，且直线BE交y轴于点G，判断△BOC与△BOG的关系，并证明你的结论；
（3）在（2）的情况下，连接OE，在x轴上是否存在点P，使以点P，B，C为顶点的△PBC与△BOE相似？如果存在，求出点P的坐标；如果不存在，说明理由．

Answer 1

分析 （1）已知A、B、D三点坐标，利用待定系数法即可确定抛物线的解析式；根据垂径定理和勾股定理可求$\widehat{AB}$所在圆的圆心坐标；
（2）点E（-2，n）是“标准锅线”中抛物线上的一点，代入抛物线的解析式可求E（-2，-$\frac{5}{3}$），根据待定系数法可求直线BE的解析式为y=$\frac{1}{3}$x-1，再根据SAS可证△BOC≌△BOG；
（3）根据直线BE：y=$\frac{1}{3}$x-1知，该直线必过（0，-1）点，那么∠EBO=∠CBO，若以点P、B、C为顶点的△PBC与△BOE相似，那么夹这组对应角的对应边必成比例，先求出BC、BO、BE的长，然后分情况根据线段间的比例关系求出BP的长，进而得到OP的长，即可确定P点坐标．

解答 解：（1）由于抛物线C₁、C₂都过点A（-3，0）、B（3，0），
可设它们的解析式为：y=a（x-3）（x+3）；
抛物线C1还经过D（0，-3），则有：-3=a（0-3）（0+3），解得a=$\frac{1}{3}$．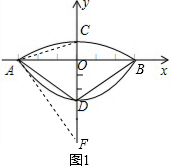
即：抛物线C₁：y=$\frac{1}{3}$x²-3（-3≤x≤3）；
如图1，连结AC，AC的垂直平分线交y轴于F，连结AF，
设OD=x，则AF=CF=x+1，
在Rt△AOF中，x²+3²=（x+1）²，解得x=4，
故$\widehat{AB}$所在圆的圆心坐标为（0，-4）；
（2）△BOC≌△BOG．
∵点E（-2，n）是“标准锅线”中抛物线上的一点，
∴n=$\frac{1}{3}$×（-2）²-3=-$\frac{5}{3}$，
∴E（-2，-$\frac{5}{3}$），
设直线BE的解析式为y=kx+b（k≠0），将点B（3，0），点E（-2，-$\frac{5}{3}$）代入直线方程中，得$\left\{\begin{array}{l}{3k+b=0}\\{-2k+b=-\frac{5}{3}}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=-1}\end{array}\right.$．
∴直线BE的解析式为y=$\frac{1}{3}$x-1．
如图2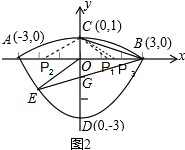，令x=0，得y=-1，
∴G（0，-1），
∴OG=OC，
又∵BA⊥CG，OB=OB，
在△BOC与△BOG中，
$\left\{\begin{array}{l}{OG=OC}\\{∠BOC=∠BOG}\\{OB=OB}\end{array}\right.$，
∴△BOC≌△BOG（SAS）；
（3）如图2，由于直线BE：y=$\frac{1}{3}$x-1必过（0，-1），所以∠CBO=∠EBO（tan∠CBO=tan∠EBO=$\frac{1}{3}$）；
由E点坐标可知：tan∠AOE≠$\frac{1}{3}$，即∠AOE≠∠CBO，所以它们的补角∠EOB≠∠CBx；
若以点P、B、C为顶点的△PBC与△BOE相似，只需考虑两种情况：
①∠CBP₁=∠EBO，且OB：BE=BP₁：BC，即：
3：$\frac{5\sqrt{10}}{3}$=BP₁：$\sqrt{10}$，得：BP₁=$\frac{9}{5}$，OP₁=OB-BP₁=$\frac{6}{5}$；
∴P₁（$\frac{6}{5}$，0）；
②∠P₂BC=∠EBO，且BC：BP₂=OB：BE，即：$\sqrt{10}$：BP₂=3：$\frac{5\sqrt{10}}{3}$，得：BP₂=$\frac{50}{9}$，OP₂=BP₂-OB=$\frac{23}{9}$；
∴P₂（-$\frac{23}{9}$，0）．
综上所述，符合条件的P点有：P₁（$\frac{6}{5}$，0）、P₂（-$\frac{23}{9}$，0）．

点评 考查了二次函数综合题．该题的难度和计算量都比较大，关键是熟练掌握函数解析式的确定、相似三角形的判定和性质等重点知识；解答（2）题时，应注意分不同的对应边来进行讨论，以免漏解．