
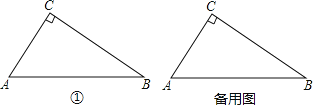
����Ŀ����ͼ�����ڡ�ABC�У���C��90�㣬AC��15��BC��20��������C����O���ABC��ÿ���߶��ཻ����O��AC�ߵ���һ��������ΪD����BC�ߵ���һ��������ΪE����AB�ߵ�����������ֱ�ΪF��G������O�İ뾶Ϊr��
��������֪��
��1���������⣬����Բ����ͼ��������һ��������������O�������������ĸ��
������̽����
��2����֤��CD2+CE2��4r2��
��3����r��8ʱ����CD2+CE2+FG2�����ֵΪ�� ����
���������
��4��ֱ��д�����������r��ȡֵ��Χ�����ڷ�Χ��ÿһ��ȷ����r��ֵ��CD2+CE2+FG2�������ֵ��ÿһ�����ֵ��Ӧ��Բ��O���γɵ�·����Ϊ�� ����
���𰸡���1�������������2�������������3��48����4��![]() ��
��
��������
��1������Ҫ��ͼ�μ��ɣ���ͼ����ʾ����
��2����ͼ���У�����![]() �����ù��ɶ������ɽ�����⣻
�����ù��ɶ������ɽ�����⣻
��3����Ϊ![]() �Ƕ�ֵ��
�Ƕ�ֵ��![]() ��
��![]() ���ң�
���ң�![]() �İ뾶Ϊ��ֵ 8���������ľ�ԽС����
�İ뾶Ϊ��ֵ 8���������ľ�ԽС����![]() Խ����Բ��
Խ����Բ��![]() ����
����![]() ΪԲ��8Ϊ�뾶��Բ�ϣ���
ΪԲ��8Ϊ�뾶��Բ�ϣ���![]() ʱ��
ʱ��![]() ��
��![]() ������̣���ʱ
������̣���ʱ![]() ����ɴ˼��ɽ�����⣻
����ɴ˼��ɽ�����⣻
��4������ȷ��![]() �ķ�Χ��Բ�ľ���
�ķ�Χ��Բ�ľ���![]() ���ʱ
���ʱ![]() ��ֵ����뾶�Ƚ�Сʱ��
��ֵ����뾶�Ƚ�Сʱ��![]() ��
��![]() ��ʱ
��ʱ![]() ��ֵ���Բ����
��ֵ���Բ����![]() �ϣ�Բ���þ�����
�ϣ�Բ���þ�����![]() ʱ����
ʱ����![]() ����
����![]() ��
��![]() ������
������![]() �����
�����![]() ����
����![]() ʱ����
ʱ����![]() ����
����![]() �ϣ���
�ϣ���![]() ����Բ�ڣ�Բ����
����Բ�ڣ�Բ����![]() ���ཻ���Ƴ���ʱԲ��Ӧ������
���ཻ���Ƴ���ʱԲ��Ӧ������![]() �д����ϣ��Ƴ�
�д����ϣ��Ƴ�![]() ʱ��
ʱ��![]() ��
��![]() �ϣ�
�ϣ�![]() ʱ��
ʱ��![]() ��
��![]() �д����ϣ���
�д����ϣ���![]() ��ֵ����Ƴ�
��ֵ����Ƴ�![]() ·������ͼ����
·������ͼ����![]() ��
��
��1���⣺��ͼ����Ϊ����
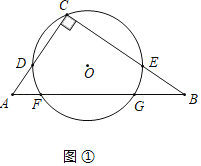
��2��֤������ͼ���У�����DE��
�ߡ�DCE��90�㣬
��DEΪ��Oֱ������DE��2r��
��CD2+CE2��DE2��4r2��

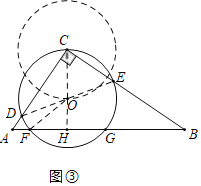
��3���⣺��ͼ���У�
��CD2+CE2�Ƕ�ֵ��FG����O���ң���O�İ뾶Ϊ��ֵ 8��
�����ľ�ԽС����FGԽ����Բ��O����CΪԲ��8Ϊ�뾶��Բ�ϣ�
��CO��ABʱ��O��AB������̣���ʱFG���
��![]() ��
��
��CH��![]() ��12��
��12��
��OC��8��
��OH��4��
OH��FG��
��![]() ��
��
��![]() ��
��
��CD2+CE2+FG2�����ֵ��![]() ��
��
�ʴ�Ϊ��448��
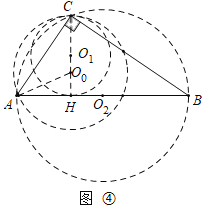
��4����ͼ���У�
����O1 ��AB����ʱ����O1��ֱ����С����СֵΪ12����ʱr��6��
��Բ��O2��AB��ʱ��Բֱ��������AB��25��
��![]() ��
��
��Բ�ľ���AB���ʱCD2+CE2+FG2��ֵ���
���뾶�Ƚ�Сʱ��O��CH��ʱCD2+CE2+FG2��ֵ���
��Բ����CH �ϣ�Բ���þ�����Aʱ����O0A��O0C��r��
��Rt��AO0H������r2����12��r��2+92��
��ã�![]() ��
��
��![]() ��
��
��![]() ʱ����O����CH�ϣ���A����Բ�ڣ�Բ����AB���ཻ��
ʱ����O����CH�ϣ���A����Բ�ڣ�Բ����AB���ཻ��
���ʱԲ��Ӧ������AC�д����ϣ�
��![]() ʱ��O��CH�ϣ�
ʱ��O��CH�ϣ�
![]() ʱ��O��AC�д����ϣ���CD2+CE2+FG2��ֵ���
ʱ��O��AC�д����ϣ���CD2+CE2+FG2��ֵ���
��O·������ͼ���� O1��O0��O2
��O1H��6��![]() ��
��
��![]() ��
��
��![]() ��AH��9��
��AH��9��
��![]() ��
��
��![]() ��
��
��O��·������![]() ��
��
�ʴ�Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������о���ƶ�����ѽ��빥��Σ�ƶ�����Ŵ�ү��ij��λ�İ���£���һƬ�µظ������ֲ������ˮ����ݮ��������ʽ�������ۣ������۵�30���У���һ������20ǧ�ˣ�Ϊ��������������ȡ�˽��۴�ʩ���Ժ�ÿ���ǰһ�������4ǧ�ˣ���x����ۼ�ΪyԪ/ǧ�ˣ�y����x�ĺ�������ʽΪ![]() �ҵ�12����ۼ�Ϊ32Ԫ/ǧ�ˣ���26����ۼ�Ϊ25Ԫ/ǧ�ˣ���֪��ֲ������ݮ�ij�ľ��18Ԫ/ǧ�ˣ�ÿ���������WԪ������=�������멁�ɱ�����
�ҵ�12����ۼ�Ϊ32Ԫ/ǧ�ˣ���26����ۼ�Ϊ25Ԫ/ǧ�ˣ���֪��ֲ������ݮ�ij�ľ��18Ԫ/ǧ�ˣ�ÿ���������WԪ������=�������멁�ɱ�����
��1��m=�� ����n=�� ����
��2����������ݮ�ڼ���ʱ����������������������Ƕ��٣�
��3����������ݮ��30���У�����������870Ԫ�Ĺ��ж����죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������
��ͼ1���ڱ߳�Ϊ1�������������У����Ӹ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��ֵ.
��ֵ.
��������
��һ����ǵ����Ǻ���ֵ������������Ҫ�ҳ����������һ��ֱ��������.�۲췢��������![]() ����ֱ���������У����dz�����������ƽ���ߵȷ��������������.�������Ӹ��
����ֱ���������У����dz�����������ƽ���ߵȷ��������������.�������Ӹ��![]() ��
��![]() ���ɵ�
���ɵ�![]() ����
����![]() ������
������![]() ����ô
����ô![]() �ͱ任����
�ͱ任����![]() .
.
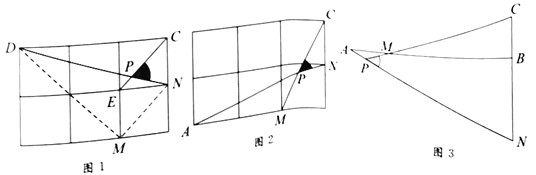
������
��1��ֱ��д��ͼ1��![]() ��ֵΪ_________��
��ֵΪ_________��
��2����ͼ2���ڱ߳�Ϊ1�������������У�![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��ֵ��
��ֵ��
˼ά��չ
��3����ͼ3��![]() ��
��![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ���ӳ�
���ӳ�![]() ��
��![]() ��ʹ
��ʹ![]() ������
������![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����������������������
����������������������![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������Ч������ʡ�ٴ���Ŀ֮һ�Ĺ����������������������ߡ�ȫ�渴���������跽ͨ����������ʩ����ƣ��Ӵ��ʵ���Ͷ�����ֲ�ǰ�ڵ���Ĺ��������Ա�֤������Ŀ���ʵ�֡����������д����IJ�����Ҫ���䡣ij������������Ϊ8�֡�10�ֵĿ�����12����ȫ����������һ�ο�������110�ֲ�����
��1����ó�����������Ϊ8�֡�10�ֵĿ�������������
��2�����Ź��̵Ľ�չ���ó�����Ҫһ���������������165�֣�Ϊ��������ó������¹��������ֿ�����6����������������Ϊ8�ֵĿ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ԫ������!����ij�̳���ƵĴ�������£���һ�����������������3����ͬ�Ŀ�Ƭ����Ƭ�Ϸֱ������10Ԫ������20Ԫ������30Ԫ�����������涨���ڱ��̳�ͬһ���ڣ��˿�ÿ������300Ԫ���Ϳ���������������һ�ſ�Ƭ������Ǯ����Żأ��ٴ�������һ�ſ�Ƭ���̳��������ſ�Ƭ������ĺͷ�����ȼ۸�Ĺ���ȯ������ȯ�����ڱ��̳����ѣ�ij�˿պ�����300Ԫ��
��1���ù˿����ɵõ��� ��Ԫ����ȯ��
��2�������û���״ͼ���б��ķ���������ù˿�����ù���ȯ�Ľ�����40Ԫ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У���E��F�ڶԽ���BD�ϣ���BE��DF����֤��
��1����ABE�ա�CDF��
��2���ı���AECF��ƽ���ı��Σ�
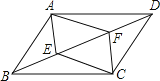
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���Ӽ�ȥ��ѧ���Ȳ���һ��·����ʱ����������ﹲ�������������ѧУʱ�ٵ���7min������ʻ��·��![]() (��λ��
(��λ��![]() )��ʱ��
)��ʱ��![]() (��λ��
(��λ��![]() )�Ĺ�ϵ��ͼ����������ʱֱ���ﹲ������(�����ﳵ�ٶ���ͬ)��������˵����ȷ����( )
)�Ĺ�ϵ��ͼ����������ʱֱ���ﹲ������(�����ﳵ�ٶ���ͬ)��������˵����ȷ����( )
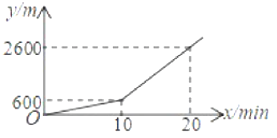
A.С����ٵ�2min��УB.С���պð�ʱ��У
C.С��������ǰ1min��УD.С��������ǰ2min��У
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪˫����y=![]() ��ֱ��y=-x+2��P��˫���ߵ�һ������һ���㣬��P��y���ƽ���ߣ���ֱ��y=-x+2��Q�㣬OΪ����ԭ�㣮
��ֱ��y=-x+2��P��˫���ߵ�һ������һ���㣬��P��y���ƽ���ߣ���ֱ��y=-x+2��Q�㣬OΪ����ԭ�㣮
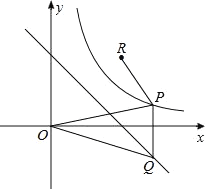

��1����ֱ��y=-x+2��������Χ�������ε��ܳ���
��2������PQO�����ΪS����S����Сֵ��
��3���趨��R��2��2�����Ե�PΪԲ�ģ�PRΪ�뾶����P�����P��ֱ��y=-x+2����M��N���㣮
���жϵ�Q���P��λ�ù�ϵ����˵�����ɣ�
����S��MON=S��PMNʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������˿��Ƶĵ����ֱ���2��5��6��8����������ͬ�⣬�����ͬ��������ϴ�Ⱥ��泯�Ϸ�������
��1�������������ȡһ���ƣ��������Ƶĵ�����ż���ĸ���Ϊ�� ����
��2���������ȡһ���Ʋ��Żأ������ٳ�ȡһ���ƣ������б�������״ͼ����ֻѡ����һ�֣���ʾ�����п��ܳ��ֵĽ�����������������Ƶĵ�������ż���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com