
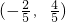 ,E为直径
,E为直径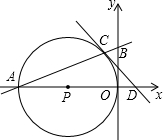 OA上一动点(与点O、A不重合).EF⊥AB于点F,交y轴于点G.设点E的横坐标为x,△BGF的面积为y.
OA上一动点(与点O、A不重合).EF⊥AB于点F,交y轴于点G.设点E的横坐标为x,△BGF的面积为y.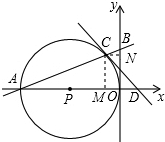 解:(1)如图:
解:(1)如图: ,CN=
,CN= .
. ,
, +
+ =2.
=2.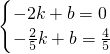 ,
, ,b=1,
,b=1,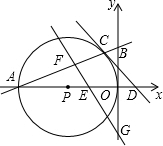
 x+1;
x+1; x+1,
x+1, =
= ,
, ,
,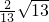 ,cos∠FGB=
,cos∠FGB=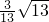 ,而E(x,0),
,而E(x,0), x,
x,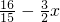 ,
, •BF•GF=
•BF•GF=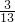 (
(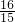 -
- x)2.
x)2. ,CN=
,CN= ,根据已知可以知道OM=CN,然后证明△ACM∽△COM,利用对应边成比例可以求出AM,然后求出A的坐标,再利用待定系数法可以求出直线AB的解析式;
,根据已知可以知道OM=CN,然后证明△ACM∽△COM,利用对应边成比例可以求出AM,然后求出A的坐标,再利用待定系数法可以求出直线AB的解析式;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 2 |
| 5 |
| 4 |
| 5 |
 OA上一动点(与点O、A不重合).EF⊥AB于点F,交y轴于点G.设点E的横坐标为x,△BGF的面积为y.
OA上一动点(与点O、A不重合).EF⊥AB于点F,交y轴于点G.设点E的横坐标为x,△BGF的面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.BF,CE相交于点O.
已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.BF,CE相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com