
���� �������С��������xֻ���ӣ�����Ա������y�����ӣ�����ÿֻ���Ӹ�8�����ӣ���ʣ20�����ӣ�ÿֻ���Ӹ�10�����ӣ���ʣ36�����ӣ��з�������⣻
�������С��������xֻ���ӣ���������8x+20��������������һԪһ�η��̽��
�۸�����������ʽ���
��� �⣺�������С��������xֻ���ӣ�����Ա������y�����ӣ�
������ã�$\left\{\begin{array}{l}{8x+20=y}\\{10x-36=y}\end{array}\right.$��
��ã�x=28��y=244��
�����С��������28ֻ���ӣ�����Ա������244�����ӣ�
�������С��������xֻ���ӣ���
8x+20=10x-36
��ã�x=28��
8��28+20=244��
�����С��������28ֻ���ӣ�����Ա������244�����ӣ�
��$\frac{20+36}{10-2}$=28��8��28+20=244��
�����С��������28ֻ���ӣ�����Ա������244�����ӣ�
���� ���⿼����һԪһ�η��̺Ͷ�Ԫһ�η������ʵ��Ӧ�ã���ϤһԪһ�η���Ӧ�����Ԫһ�η�����Ӧ���������������Ӧ������Ĺ�ϵ�ǽ������Ĺؼ���


 ��������������������ϵ�д�
��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0��AB��2 | B�� | 2��AB��10 | C�� | 2��AB��12 | D�� | 2��AB��22 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
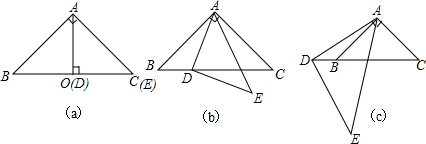
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | ��80��ͼ�� | B�� | ��82��ͼ�� | C�� | ��72��ͼ�� | D�� | ��95��ͼ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com