
����Ŀ�����������������A��B�����ͺŵ�LED���ܵƹ�200յ���ۣ���֪ÿյA��B�����ͺŵ�LED���ܵƵĽ��۷ֱ�Ϊ18Ԫ��45Ԫ���ⶨ�ۼ۷ֱ�Ϊ28Ԫ��60Ԫ��
��1�������������ƻ�����������LED���ܵƺ��ܻ���2200Ԫ���ʼס�������LED���ܵ�Ӧ�ֱ�����յ��
��2�������������ƻ�Ͷ���ʽ���6900Ԫ��������������LED���ܵƺ����������2600Ԫ���������ļ��ֹ�����������̽�����ֹ��������������
���𰸡���1����������LED���ܵ�160յ����������LED���ܵ�40յ����2���𰸼�����.
�������������������1���蹺�������ܵ�xյ�����������ܵ�yյ�����ݹ���A��B�����ͺŵ��ܵƹ�200յ�����������ܵƺ��ܻ���2200Ԫ�з�������⼴�ɣ�
��2���蹺�������ܵ�aյ���������ܵ�յ������Ͷ���ʽ���6900Ԫ���������������ܵƺ����������2600Ԫ�в���ʽ�����a�ķ�Χ������aΪ������Ӷ��ɵý����������ٷֱ����ÿ�ַ��������ȽϺɵ���
�����������1���蹺������LED���ܵ�xյ����������LED���ܵ�yյ��
�������⣬�ã�![]() ��
��
��ã�![]() ��
��
�𣺹�������LED���ܵ�160յ����������LED���ܵ�40յ��
��2���蹺������LED���ܵ�aյ��������LED���ܵ�յ��
�������⣬�ã�![]() ��
��
��ã�77![]() ��a��80��
��a��80��
��a������
����������������֣�
�ٹ�������LED���ܵ�78յ��������LED���ܵ�122յ����ʱ����Ϊ��78��10+122��15=2610��Ԫ����
�ڹ�������LED���ܵ�79յ��������LED���ܵ�121յ����ʱ����Ϊ��79��10+121��15=2605��Ԫ����
�۹�������LED���ܵ�80յ��������LED���ܵ�120յ����ʱ����Ϊ��80��10+120��15=2600��Ԫ����
�ʷ����ٻ������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ķ����н�����̣��ٷ���������⣮
��֪x2+x-1=0����x3+2x2+3��ֵ��
�⣺x3+2x2+3=x3+x2-x+x2+x+3
=x��x2+x-1��+x2+x-1+4
=0+0+4=4
���1+x+x2+x3=0����x+x2+x3+x4+x5+x6+x7+x8��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼAB��CD�ཻ�ڵ�O��AO��BO��AC��DB����ôOC��OD�����˵��������ɡ�С���Ľ���������£�����˵��ÿһ�������ɡ�

�⣺OC��OD���������£�
��AC��DB�� ��
���A=��B����C=��D�� ��
�ڡ�AOC�͡�BOD��

���AOC�ա�BOD �� ��
��OC��OD�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е�ʽ�����ҵı��Σ�������ʽ�ֽ���ǣ� ��
A.a��x��y��=ax��ay
B.x2+2x+1=x��x+2��+1
C.��x+1����x+3��=x2+4x+3
D.x3��x=x��x+1����x��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABC�DZ߳�Ϊ4cm�ĵȱ������Σ�����P��Qͬʱ��A��B����������ֱ���AB��BC���������ƶ������ǵ��ٶȶ���1cm/s������P�����Bʱ��P��Q����ֹͣ�˶������P���˶�ʱ��t(s)��������и����⣺
��1����![]() �����;
�����;
��2����tΪ��ֵ�ǣ���PBQ��ֱ�������Σ�
��3��̽�����Ƿ����ijһʱ��t��ʹ�ı���APQC�������![]() ����İ˷�֮�壿������ڣ����t��ֵ����������˵������.
����İ˷�֮�壿������ڣ����t��ֵ����������˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������������У�������
�ٶԶ�����ȣ�����ֱ��ƽ�У��ڴ�����ȣ���������Ƕ�Ӧ��ȵ�����ֱ��������ȫ�ȣ�������������ֱ�ǵ��ı����Ǿ��Σ���ƽ���ҵ�ֱ����ֱ���ң�����ƽ�������ԵĻ���
A. .1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪A��a��0����B��b��0��������a��b����|a+1|+��b��3��2=0��
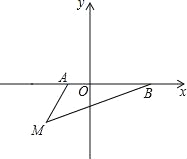
��1����գ�a=������b=������
��2������ڵ�����������һ��M����2��m�������ú�m��ʽ�ӱ�ʾ��ABM�������
��3���ڣ�2�������£���m=![]() ʱ����y������һ��P��ʹ����BMP���������ABM�������ȣ��������P�����꣮
ʱ����y������һ��P��ʹ����BMP���������ABM�������ȣ��������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3�֣��ҹ����ٹ�·��չѸ�٣��ݱ�������ĿǰΪֹ��ȫ�����ٹ�·�����ԼΪ10��8��ǧ�ף�10��8���ÿ�ѧ��������ʾΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com