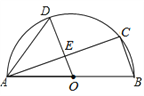
【题目】如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E.
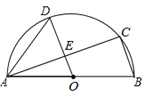
（1）若∠B=70°,求弧CD的度数；
（2）若AB=26，DE=8，求AC的长.
【答案】（1）
的度数是70°；(2) AC=24.
【解析】试题分析：（1）根据圆周角定理可得∠ACB=90°，则可得∠CAB的度数，由OD∥BC，可得∠AOD的度数，又OD=OA，从而可得∠OAD的度数，从而得到∠DAC的度数，继而得到弧CD的度数；
（2）易证OE是△ABC的中位线，由DE的长可得OE的长，利用中位线定理求得BC的长，由勾股定理即可得AC的长．
试题解析：（1）∵AB是直径，∴∠C=90°，∵∠B=70°，∴∠BAC=20°，
∵OD∥BC，∴∠AOD=∠B=70°，又OD=OA，∴∠OAD=55°，
∴∠DAC=35°，∴
的度数是70°；
(2)∵AB=26，∴OD=13，又DE=8，∴OE=5，
∵OD∥BC，OA=OB，∴BC=2OE=10，又∵∠C=90°，∴AC=
=24.
科目：初中数学 来源： 题型：
【题目】如图：在平面直角坐标系中A(3，2)，B(4，3)，C(1，1)．
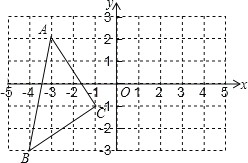
（1）在图中作出△ABC关于y轴对称图形△A1B1C1；
（2）写出A1、B1、C1的坐标分别是A1(___，___)，B1(___，___)，C1(___，___)；
（3）△ABC的面积是___．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一次函数y=kx﹣1的图象经过点P，且y的值随x值的增大而增大，则点P的坐标可以为（ ）
A. （﹣5，3） B. （1，﹣3） C. （2，2） D. （5，﹣1）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD⊥BC，EF垂直平分AC，交AC于点F，交BC于点E，且BD=DE．
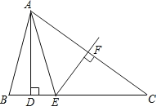
（1）若∠BAE=40°，求∠C的度数；
（2）若△ABC周长为15cm，AC=6cm，求DC长．
查看答案和解析>>
科目：初中数学 来源： 题型：
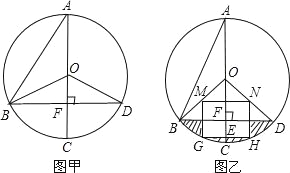
【题目】如图甲，已知在⊙O中，AB=
，AC是⊙O的直径，AC⊥BD于F，∠A=30度．
（1）连接BC，CD，请你判定四边形OBCD是何种特殊的四边形？试说明理由；
（2）若用扇形OBD围成一个圆锥侧面，请求出这个圆锥的底面圆的半径；
（3）如图乙，若将“∠A=30°”改为“∠A=22.5°”，其余条件不变，以半径OB、OD的中点M、N为顶点作矩形MNGH，顶点G、H在⊙O的劣弧
上，GH交OC于点E．试求图中阴影部分的面积．（结果保留π）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD是圆O的切线，切点为A，AB是圆O的弦。过点B作BC//AD，交圆O于点C，连接AC，过点C作CD//AB，交AD于点D。连接AO并延长交BC于点M，交过点C的直线于点P，且BCP=ACD。
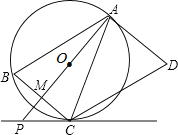
（1）判断直线PC与圆O的位置关系，并说明理由：
（2） 若AB=9，BC=6，求PC的长。
查看答案和解析>>
科目：初中数学 来源： 题型：
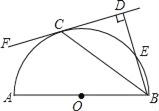
【题目】如图，AB是半圆O的直径，C是半圆O上的一点，CF切半圆O于点C，BD⊥CF于为点D，BD与半圆O交于点E．
(1)求证：BC平分∠ABD．
(2)若DC=8，BE=4，求圆的直径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的弦，AB=2，点C在
上运动，且∠ACB=30°.
（1）求⊙O的半径；
（2）设点C到直线AB的距离为x，图中阴影部分的面积为y，求y与x之间的函数关系，并写出自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙O中，AB是⊙O的直径，G为弦AE的中点，连接OG并延长交⊙O于点D，连接BD交AE于点F，延长AE至点C，使得FC=BC，连接BC．
(1)求证：BC是⊙O的切线；
(2)⊙O的半径为5，tanA=
，求FD的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com