
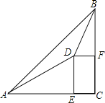
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=2.点P是△ABC内部的一个动点,且满足∠PAC=∠PCB,则线段BP长的最小值是_____.

科目:初中数学 来源: 题型:
【题目】如图,登山队员在山脚![]() 点测得山顶
点测得山顶![]() 点的仰角为
点的仰角为![]() ,当沿倾斜角为
,当沿倾斜角为![]() 的斜坡前进
的斜坡前进![]() 到达
到达![]() 点以后,又在
点以后,又在![]() 点测得山顶
点测得山顶![]() 点的仰角为
点的仰角为![]() ,山的高度
,山的高度![]() ________.(精确到
________.(精确到![]() 米)
米)
查看答案和解析>>
科目:初中数学 来源: 题型:
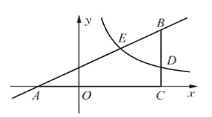
【题目】已知![]() 的边
的边![]() 与x轴重合,
与x轴重合,![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象与
在第一象限内的图象与![]() 边交于点
边交于点![]() ,与AB边交于点
,与AB边交于点![]() ,
,![]() 的面积为2.
的面积为2.
(1)直接写出![]() 之间的数量关系 ;当
之间的数量关系 ;当![]() 时,求反比例函数及直线
时,求反比例函数及直线![]() 的表达式;
的表达式;
(2)设直线![]() 与y轴交于点F,点P在射线FD上,在(1)的条件下,如果
与y轴交于点F,点P在射线FD上,在(1)的条件下,如果![]() 与
与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人用如图的两个分格均匀的转盘![]() 、
、![]() 做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
![]() 用列表格或画树状图的方法表示游戏所有可能出现的结果.
用列表格或画树状图的方法表示游戏所有可能出现的结果.
![]() 求甲、乙两人获胜的概率.
求甲、乙两人获胜的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共![]() 个,某学习小组做摸球试验,将球搅匀后,从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
个,某学习小组做摸球试验,将球搅匀后,从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
![]() 请估计:当
请估计:当![]() 很大时,摸到白球的频率将会接近于多少?
很大时,摸到白球的频率将会接近于多少?
摸球的次数 |
|
|
|
|
|
|
摸到白球的次数 |
|
|
|
|
|
|
摸到白球的概率 |
|
|
|
|
|
|
![]() 假如你去摸一次,你摸到白球的可能性为多大?这时摸到黑球的可能性为多大?
假如你去摸一次,你摸到白球的可能性为多大?这时摸到黑球的可能性为多大?
![]() 试估算口袋中黑、白两种颜色的球各有多少个?
试估算口袋中黑、白两种颜色的球各有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作圆的切线.
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.
小敏的作法如下:如图,
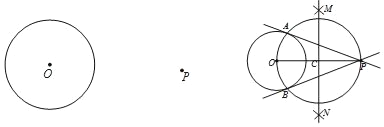
(1)连接OP,作线段OP的垂直平分线MN交OP于点C.
(2)以点C为圆心,CO的长为半径作圆,交⊙O于A,B两点.
(3)作直线PA,PB.
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是 ;由此可证明直线PA,PB都是⊙O的切线,其依据是 .请写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论:
①抛物线y=ax2(a≠0)的图象的顶点一定是原点;
②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当-3<x<2时,ax2+kx<b,
其中正确的结论是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
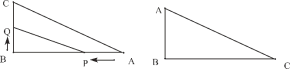
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 边
边![]() ,
,![]() 上的两个动点,其中点
上的两个动点,其中点![]() 以每秒2个单位的速度由点
以每秒2个单位的速度由点![]() 向点
向点![]() 运动;点
运动;点![]() 以每秒3个单位的速度由点
以每秒3个单位的速度由点![]() 到点
到点![]() 再到点
再到点![]() 运动;它们同时出发,当一个点到达终点停止,另一个点继续运动到终点也停止,设运动时间为
运动;它们同时出发,当一个点到达终点停止,另一个点继续运动到终点也停止,设运动时间为![]() 秒。
秒。
(1)求![]() 的面积。
的面积。
(2)当点![]() 在边
在边![]() 上运动时,出发几秒后,
上运动时,出发几秒后,![]() 是等腰三角形。
是等腰三角形。
(3)当点![]() 在边
在边![]() 上运动时,出发几秒后,
上运动时,出发几秒后,![]() 是等腰三角形。
是等腰三角形。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com