
【题目】已知![]() 的边
的边![]() 与x轴重合,
与x轴重合,![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象与
在第一象限内的图象与![]() 边交于点
边交于点![]() ,与AB边交于点
,与AB边交于点![]() ,
,![]() 的面积为2.
的面积为2.
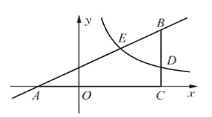
(1)直接写出![]() 之间的数量关系 ;当
之间的数量关系 ;当![]() 时,求反比例函数及直线
时,求反比例函数及直线![]() 的表达式;
的表达式;
(2)设直线![]() 与y轴交于点F,点P在射线FD上,在(1)的条件下,如果
与y轴交于点F,点P在射线FD上,在(1)的条件下,如果![]() 与
与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
【答案】(1) n=2m;反比例函数的解析式为y=![]() ,直线AB的函数解析式为y=
,直线AB的函数解析式为y=![]() x+1.
x+1.
(2) (1,1)或(5,1).
【解析】
(1)将D(4,m)、E(2,n)代入反比例函数![]() 解析式,进而得出n,m的关系;利用△BDE的面积为2,得出m的值,进而得出D,E,B的坐标,利用待定系数法求出一次函数与反比例函数关系式即可;
解析式,进而得出n,m的关系;利用△BDE的面积为2,得出m的值,进而得出D,E,B的坐标,利用待定系数法求出一次函数与反比例函数关系式即可;
(2)利用△AEO与△EFP 相似存在两种情况,分别利用图形分析得出即可.
(1)∵D(4,m)、E(2,n)在反比例函数![]() 的图象上,
的图象上,
∴![]() .
.
整理,得n=2m;
如图1,过点E作EH⊥BC,垂足为H.
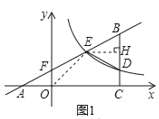
在Rt△BEH中,tan∠BEH=tan∠A=![]() ,
,
因为EH=2,所以BH=1.
因此D(4,m),E(2,2m),B(4,2m+1).
已知△BDE的面积为2,
所以![]() BD·EH=
BD·EH=![]() (m+1)×2=2.
(m+1)×2=2.
解得m=1.
因此D(4,1),E(2,2),B(4,3).
因为点D(4,1)在反比例函数![]() 的图象上,
的图象上,
所以k=4.
因此反比例函数的解析式为y=![]() ,
,
设直线AB的解析式为y=kx+b,代入B(4,3)、E(2,2),
得![]() ,
,
解得![]() ,
,
因此直线AB的函数解析式为y=![]() x+1.
x+1.
(2)∵AB解析式为y=![]() x+1.
x+1.
∴A(-2,0),F(0,1),又D(4,1),E(2,2),B(4,3).
∴AE=2![]() ,EF=
,EF=![]()
因为直线y=![]() x+1与y轴交于点F(0,1),点D的坐标为(4,1),
x+1与y轴交于点F(0,1),点D的坐标为(4,1),
所以FD∥x轴,∠EFP=∠EAO.
因此△AEO与△EFP 相似存在两种情况:
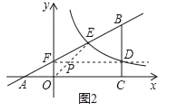
①如图2,当![]() 时,
时,![]()
解得FP=1.此时点P的坐标为(1,1).
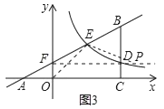
②如图3,当![]() 时,
时,![]() .
.
解得FP=5.
此时点P的坐标为(5,1).
综上所述,P点坐标为:(1,1)或(5,1).


科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35 m的速度沿着与水平方向成75°角的方向飞行,40 min时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为45°,求A庄与B庄的距离及山高(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图1,2).请根据统计图解答下列问题:

(1)本次调查中,王老师一共调查了 名学生;
(2)将条形统计图补充完整;
(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,![]() 且
且![]() 于点E,与CD相交于点F,
于点E,与CD相交于点F,![]() 于点H,交BE于点G.下列结论:①BD=CD;②AD+CF=BD;③
于点H,交BE于点G.下列结论:①BD=CD;②AD+CF=BD;③![]() ;④AE=CF.其中正确的是____________(填序号)
;④AE=CF.其中正确的是____________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①一事件发生的概率不可能大于![]() ;②大量试验中事件发生的频率就是事件发生的概率;③若一堆产品的合格率为
;②大量试验中事件发生的频率就是事件发生的概率;③若一堆产品的合格率为![]() ,则从中任取
,则从中任取![]() 件就一定有
件就一定有![]() 件合格品,
件合格品,![]() 件次品;④用列举法求概率时列举出来的所有可能的结果应该是等可能的
件次品;④用列举法求概率时列举出来的所有可能的结果应该是等可能的
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=2.点P是△ABC内部的一个动点,且满足∠PAC=∠PCB,则线段BP长的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( ).
A.在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线
B.到点![]() 距离等于
距离等于![]() 的点的轨迹是以点
的点的轨迹是以点![]() 为圆心,半径长为
为圆心,半径长为![]() 的圆
的圆
C.到直线![]() 距离等于
距离等于![]() 的点的轨迹是两条平行于
的点的轨迹是两条平行于![]() 且与
且与![]() 的距离等于
的距离等于![]() 的直线
的直线
D.等腰三角形![]() 的底边
的底边![]() 固定,顶点
固定,顶点![]() 的轨迹是线段
的轨迹是线段![]() 的垂直平分线
的垂直平分线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com