
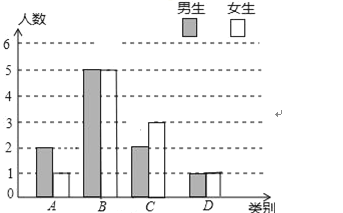
ЁОЬтФПЁПбЇаЃЪЕЪЉаТПЮГЬИФИявдРДЃЌбЇЩњЕФбЇЯАФмСІгаСЫКмДѓЬсИпЃЎЭѕРЯЪІЮЊНјвЛВНСЫНтБОАрбЇЩњзджїбЇЯАЁЂКЯзїНЛСїЕФЯжзДЃЌЖдИУАрВПЗжбЇЩњНјааЕїВщЃЌАбЕїВщНсЙћЗжГЩЫФРрЃЈAЃКЬиБ№КУЃЌBЃККУЃЌCЃКвЛАуЃЌDЃКНЯВюЃЉКѓЃЌдйНЋЕїВщНсЙћЛцжЦГЩСНЗљВЛЭъећЕФЭГМЦЭМЃЈШчЭМ1,2ЃЉЃЎЧыИљОнЭГМЦЭМНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉБОДЮЕїВщжаЃЌЭѕРЯЪІвЛЙВЕїВщСЫЁЁ ЁЁУћбЇЩњЃЛ
ЃЈ2ЃЉНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉЮЊСЫЙВЭЌНјВНЃЌЭѕРЯЪІДгБЛЕїВщЕФAРрКЭDРрбЇЩњжаЗжБ№бЁШЁвЛУћбЇЩњНјааЁАБјНЬБјЁБЛЅжњбЇЯАЃЌЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓГіЧЁКУбЁжавЛУћФаЩњКЭвЛУћХЎЩњЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ20ЃЛЃЈ2ЃЉзїЭММћЪдЬтНтЮіЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩAРрЕФбЇЩњЪ§вдМАЫљеМЕФАйЗжБШМДПЩЧѓЕУД№АИЃЛ
ЃЈ2ЃЉЯШЧѓГіCРрЕФХЎЩњЪ§ЁЂDРрЕФФаЩњЪ§ЃЌМЬЖјПЩВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉЪзЯШИљОнЬтвтСаГіБэИёЃЌдйРћгУБэИёЧѓЕУЫљгаЕШПЩФмЕФНсЙћгыЧЁКУбЁжавЛУћФаЩњКЭвЛУћХЎЩњЕФЧщПіЃЌМЬЖјЧѓЕУД№АИЃЎ
ЃЈ1ЃЉИљОнЬтвтЕУЃКЭѕРЯЪІвЛЙВЕїВщбЇЩњЃКЃЈ2+1ЃЉЁТ15%=20ЃЈУћЃЉЃЛ
ЙЪД№АИЮЊ20ЃЛ
ЃЈ2ЃЉЁпCРрХЎЩњЃК20ЁС25%Љ2=3ЃЈУћЃЉЃЛ
DРрФаЩњЃК20ЁСЃЈ1Љ15%Љ50%Љ25%ЃЉЉ1=1ЃЈУћЃЉЃЛ
ШчЭМЃК
ЃЈ3ЃЉСаБэШчЯТЃКAРржаЕФСНУћФаЩњЗжБ№МЧЮЊA1КЭA2ЃЌ
ФаA1 | ФаA2 | ХЎA | |
ФаD | ФаA1ФаD | ФаA2ФаD | ХЎAФаD |
ХЎD | ФаA1ХЎD | ФаA2ХЎD | ХЎAХЎD |
ЙВга6жжЕШПЩФмЕФНсЙћЃЌЦфжаЃЌвЛФавЛХЎЕФга3жжЃЌЫљвдЫљбЁСНЮЛЭЌбЇЧЁКУЪЧвЛЮЛФаЩњКЭвЛЮЛХЎЩњЕФИХТЪЮЊЃК![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
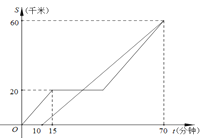
ЁОЬтФПЁПМзЁЂввСНГЕЖМДгAЕиЧАЭљBЕиЃЌШчЭМЗжБ№БэЪОМзЁЂввСНГЕРыAЕиЕФОрРыSЃЈЧЇУзЃЉгыЪБМфtЃЈЗжжгЃЉЕФКЏЪ§ЙиЯЕ.вбжЊМзГЕГіЗЂ10ЗжжгКѓввГЕВХГіЗЂЃЌМзГЕжаЭОвђЙЪЭЃжЙааЪЛвЛЖЮЪБМфКѓАДдЫйМЬајЪЛЯђBЕиЃЌзюжеМзЁЂввСНГЕЭЌЪБЕНДяBЕиЃЌИљОнЭМжаЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉМзЁЂввСНГЕааЪЛЪБЕФЫйЖШЗжБ№ЮЊЖрЩйЃП
ЃЈ2ЃЉввГЕГіЗЂЖрЩйЗжжгКѓЕквЛДЮгыМзГЕЯргіЃП
ЃЈ3ЃЉМзГЕжаЭОвђЙЪеЯЭЃжЙааЪЛЕФЪБМфЮЊЖрЩйЗжжгЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКвЛИіе§БШР§КЏЪ§ЭМЯѓyЃН2xКЭвЛИівЛДЮКЏЪ§yЃНkx+bЕФЭМЯѓНЛгкЕуPЃЈЉ2ЃЌaЃЉЧввЛДЮКЏЪ§ЕФЭМЯѓгыyжсЕФНЛЕуQЕФзнзјБъЮЊ4ЃЎ
ЃЈ1ЃЉЧѓетСНИіКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкЭЌвЛзјБъЯЕжаЃЌЗжБ№ЛГіетСНИіКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ3ЃЉЧѓЁїPQOЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌвбжЊЃКдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌAB=ACЃЌжБЯпmОЙ§ЕуAЃЌBDЁЭжБЯпm, CEЁЭжБЯпm,ДЙзуЗжБ№ЮЊЕуDЁЂE.жЄУї:DE=BD+CE.
ЃЈ2ЃЉ ШчЭМЃЈ2ЃЉЃЌНЋЃЈ1ЃЉжаЕФЬѕМўИФЮЊЃКдкЁїABCжаЃЌAB=ACЃЌDЁЂAЁЂEШ§ЕуЖМдкжБЯпmЩЯ,ВЂЧвгаЁЯBDA=ЁЯAEC=ЁЯBAC=![]() ,Цфжа
,Цфжа![]() ЮЊШЮвтШёНЧЛђЖлНЧ.ЧыЮЪНсТлDE=BD+CEЪЧЗёГЩСЂ?ШчГЩСЂ,ЧыФуИјГіжЄУї;ШєВЛГЩСЂ,ЧыЫЕУїРэгЩ.
ЮЊШЮвтШёНЧЛђЖлНЧ.ЧыЮЪНсТлDE=BD+CEЪЧЗёГЩСЂ?ШчГЩСЂ,ЧыФуИјГіжЄУї;ШєВЛГЩСЂ,ЧыЫЕУїРэгЩ.
ЃЈ3ЃЉЭиеЙгыгІгУЃКШчЭМЃЈ3ЃЉЃЌDЁЂEЪЧDЁЂAЁЂEШ§ЕуЫљдкжБЯпmЩЯЕФСНЖЏЕуЃЈDЁЂAЁЂEШ§ЕуЛЅВЛжиКЯЃЉ,ЕуFЮЊЁЯBACЦНЗжЯпЩЯЕФвЛЕу,ЧвЁїABFКЭЁїACFОљЮЊЕШБпШ§НЧаЮЃЌСЌНгBDЁЂCE,ШєЁЯBDA=ЁЯAEC=ЁЯBACЃЌЪдХаЖЯЁїDEFЕФаЮзД.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАДвЊЧѓзїЭМЃКвбжЊAЃЈЉ2ЃЌ1ЃЉЃЌBЃЈЉ1ЃЌ2ЃЉЃЌCЃЈЉ3ЃЌ4ЃЉЃЎ
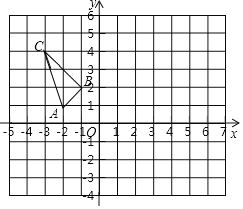
ЃЈ1ЃЉЛГігыШ§НЧаЮABCЙигкyжсЖдГЦЕФШ§НЧаЮA1B1C1ЃЛ
ЃЈ2ЃЉНЋШ§НЧаЮA1B1C1ЯШЯђгвЦНвЦ2ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ1ИіЕЅЮЛЃЌЕУЕНШ§НЧаЮA2B2C2ЃЌдђШ§НЧаЮA2B2C2ЖЅЕузјБъЗжБ№ЮЊЃКA2ЁЁ ЁЁB2ЁЁ ЁЁC2ЁЁ ЁЁЃЛ
ЃЈ3ЃЉШєЕуPЃЈa-1ЃЌb+2ЃЉгыЕуAЙигкxжсЖдГЦЃЌдђa=ЁЁ ЁЁЃЌb= ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЕФБп
ЕФБп![]() гыxжсжиКЯЃЌ
гыxжсжиКЯЃЌ![]() ЃЌЗДБШР§КЏЪ§
ЃЌЗДБШР§КЏЪ§![]() дкЕквЛЯѓЯоФкЕФЭМЯѓгы
дкЕквЛЯѓЯоФкЕФЭМЯѓгы![]() БпНЛгкЕу
БпНЛгкЕу![]() ЃЌгыABБпНЛгкЕу
ЃЌгыABБпНЛгкЕу![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ2.
ЕФУцЛ§ЮЊ2.
ЃЈ1ЃЉжБНгаДГі![]() жЎМфЕФЪ§СПЙиЯЕ ЃЛЕБ
жЎМфЕФЪ§СПЙиЯЕ ЃЛЕБ![]() ЪБЃЌЧѓЗДБШР§КЏЪ§МАжБЯп
ЪБЃЌЧѓЗДБШР§КЏЪ§МАжБЯп![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЩшжБЯп![]() гыyжсНЛгкЕуF,ЕуPдкЩфЯпFDЩЯЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌШчЙћ
гыyжсНЛгкЕуF,ЕуPдкЩфЯпFDЩЯЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌШчЙћ![]() гы
гы![]() ЯрЫЦЃЌЧѓЕу
ЯрЫЦЃЌЧѓЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
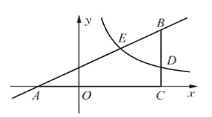
ЁОЬтФПЁПШчЭМЃЌ![]() Ш§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ
Ш§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ

ЃЈ![]() ЃЉЧыЛГіНЋ
ЃЉЧыЛГіНЋ![]() ЯђзѓЦНвЦ
ЯђзѓЦНвЦ![]() ИіЕЅЮЛГЄЖШКѓЕУЕНЕФЭМаЮ
ИіЕЅЮЛГЄЖШКѓЕУЕНЕФЭМаЮ![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉЧыЛГі
ЃЉЧыЛГі![]() ЙигкдЕу
ЙигкдЕу![]() ГЩжааФЖдГЦЕФЭМаЮ
ГЩжааФЖдГЦЕФЭМаЮ![]()
ЃЈ![]() ЃЉдк
ЃЉдк![]() жсЩЯеввЛЕу
жсЩЯеввЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФжЕзюаЁЃЌЧыжБНгаДГіЕу
ЕФжЕзюаЁЃЌЧыжБНгаДГіЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФПкДќРязАгажЛгабеЩЋВЛЭЌЕФКкЁЂАзСНжжбеЩЋЕФЧђЙВ![]() ИіЃЌФГбЇЯАаЁзщзіУўЧђЪдбщЃЌНЋЧђНСдШКѓЃЌДгжаЫцЛњУўГівЛИіЧђМЧЯТбеЩЋЃЌдйАбЫќЗХЛиДќжаЃЌВЛЖЯжиИДЃЌЯТБэЪЧЛюЖЏНјаажаЕФвЛзщЭГМЦЪ§ОнЃК
ИіЃЌФГбЇЯАаЁзщзіУўЧђЪдбщЃЌНЋЧђНСдШКѓЃЌДгжаЫцЛњУўГівЛИіЧђМЧЯТбеЩЋЃЌдйАбЫќЗХЛиДќжаЃЌВЛЖЯжиИДЃЌЯТБэЪЧЛюЖЏНјаажаЕФвЛзщЭГМЦЪ§ОнЃК
![]() ЧыЙРМЦЃКЕБ
ЧыЙРМЦЃКЕБ![]() КмДѓЪБЃЌУўЕНАзЧђЕФЦЕТЪНЋЛсНгНќгкЖрЩйЃП
КмДѓЪБЃЌУўЕНАзЧђЕФЦЕТЪНЋЛсНгНќгкЖрЩйЃП
УўЧђЕФДЮЪ§ |
|
|
|
|
|
|
УўЕНАзЧђЕФДЮЪ§ |
|
|
|
|
|
|
УўЕНАзЧђЕФИХТЪ |
|
|
|
|
|
|
![]() МйШчФуШЅУўвЛДЮЃЌФуУўЕНАзЧђЕФПЩФмадЮЊЖрДѓЃПетЪБУўЕНКкЧђЕФПЩФмадЮЊЖрДѓЃП
МйШчФуШЅУўвЛДЮЃЌФуУўЕНАзЧђЕФПЩФмадЮЊЖрДѓЃПетЪБУўЕНКкЧђЕФПЩФмадЮЊЖрДѓЃП
![]() ЪдЙРЫуПкДќжаКкЁЂАзСНжжбеЩЋЕФЧђИїгаЖрЩйИіЃП
ЪдЙРЫуПкДќжаКкЁЂАзСНжжбеЩЋЕФЧђИїгаЖрЩйИіЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊRtЁїABCжаЃЌЁЯABC=90ЁуЃЌЯШАбЁїABCШЦЕуBЫГЪБеыа§зЊ90ЁужСЁїDBEКѓЃЌдйАбЁїABCбиЩфЯпЦНвЦжСЁїFEGЃЌDEЁЂFGЯрНЛгкЕуHЃЎ

ЃЈ1ЃЉХаЖЯЯпЖЮDEЁЂFGЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉСЌНсCGЃЌЧѓжЄЃКЫФБпаЮCBEGЪЧе§ЗНаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com