
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.

(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
【答案】见解析
【解析】试题分析: (1)根据旋转和平移可得∠DEB=∠ACB,∠GFE=∠A,再根据∠ABC=90°可得∠A+∠ACB=90°,进而得到∠DEB+∠GFE=90°,从而得到DE、FG的位置关系是垂直;(2)根据旋转和平移找出对应线段和角,然后再证明是矩形,后根据邻边相等可得四边形CBEG是正方形.
试题解析:
(1)解:FG⊥ED.理由如下:
∵△ABC绕点B顺时针旋转90°至△DBE后,∴∠DEB=∠ACB,
∵把△ABC沿射线平移至△FEG,∴∠GFE=∠A,∵∠ABC=90°,
∴∠A+∠ACB=90°,∴∠DEB+∠GFE=90°,∴∠FHE=90°,∴FG⊥ED;
(2)证明:根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,
∵CG∥EB,∴∠BCG=∠CBE=90°,∴四边形BCGE是矩形,∵CB=BE,
∴四边形CBEG是正方形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己如FG⊥AB,、CD⊥AB,垂足分别为G、D,∠1=∠2.
求证:∠CED+∠ACB=180°请将下面的证明过程补充完整.
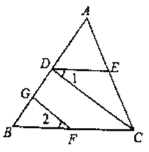
证明:∵FG⊥AB,CD⊥AB(已知),
∴∠FGB=∠CDB=90°(垂直的定义)
∴GF∥CD(___________________________)
∵GF∥CD(已证)
∴∠2=∠BCD(___________________________)
又∵∠1=∠2(已知),
∴∠1=∠BCD(___________________________)
∴___________________________,(___________________________)
∴∠CED+∠ACB=180°(___________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单 位:s)(0<t<![]() )。
)。
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有( )
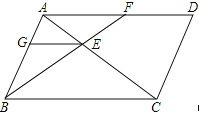
A.4对 B.5对 C.6对 D.7对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在矩形纸片
,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() ,
,![]() 也随之移动.
也随之移动.
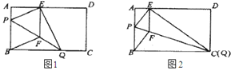
①当点![]() 与点
与点![]() 重合时(如图
重合时(如图![]() ),求菱形
),求菱形![]() 的边长;
的边长;
②若限定![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上移动,求出点
上移动,求出点![]() 在边
在边![]() 上移动的最大距离.
上移动的最大距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com