
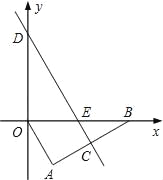
【题目】如图,在 Rt△OAB 中,∠A=90°,∠ABO=30°,OB=![]() ,边 AB的垂直平分线 CD 分别与 AB、x 轴、y 轴交于点 C、E、D.
,边 AB的垂直平分线 CD 分别与 AB、x 轴、y 轴交于点 C、E、D.
(1)求点 E的坐标;
(2)求直线 CD的解析式;
(3)在直线 CD上找一点Q使得三角形O,D,Q为等腰三角形,并求出所有的Q点;若不存在,请说明理由.
【答案】(1)E(![]() ,0);(2)y=﹣
,0);(2)y=﹣![]() x+2;(3)使得三角形 O,D,Q 为等腰三角形的Q 点 Z 坐标为 Q1(1,﹣
x+2;(3)使得三角形 O,D,Q 为等腰三角形的Q 点 Z 坐标为 Q1(1,﹣![]() +2),Q2(﹣1,
+2),Q2(﹣1,![]() +2),Q3(
+2),Q3(![]() ,1),Q4(
,1),Q4(![]() ,﹣1).
,﹣1).
【解析】
![]() 根据 DC 是 AB 垂直平分线,得出 C 点为 OB 的中点,再根据 OB 的值,即可求出点 E 的坐标;
根据 DC 是 AB 垂直平分线,得出 C 点为 OB 的中点,再根据 OB 的值,即可求出点 E 的坐标;
![]() 先过点C作 CH⊥x轴,在 Rt△ABO中,根据∠ABO 的度数和 OB 的值求出AB的长,再在 Rt△CBH 中,求出 OH 的值,得出点 D 的坐标,再设直线CD的解析式,得出 k,b的值,即可求出直线CD的解析式;
先过点C作 CH⊥x轴,在 Rt△ABO中,根据∠ABO 的度数和 OB 的值求出AB的长,再在 Rt△CBH 中,求出 OH 的值,得出点 D 的坐标,再设直线CD的解析式,得出 k,b的值,即可求出直线CD的解析式;
![]() 分三种情况讨论,分别根据Q点的不同位置求出Q的坐标即可.
分三种情况讨论,分别根据Q点的不同位置求出Q的坐标即可.
(1)∵DC 是 AB 垂直平分线,OA 垂直 AB,
∴C 点为 OB 的中点,
∵∠A=90°,∠DCB=90°,
∴OA∥CD,
∴E 为 OB 的中点,
∵![]()
∴![]()
∴![]()
(2)过点 C 作 CH⊥x 轴于点 H,
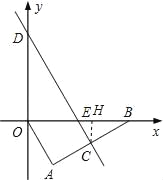
在 Rt△ABO 中,∠ABO=30°,![]()
![]()
![]()
又∵CD 垂直平分 AB,
∴BC=1,在 Rt△CBH 中,![]()
![]()
∴![]()
∴![]()
∵∠DGO=60°,
∴![]()
∴![]()
∴![]()
设直线 CD 的解析式为:y=kx+b,则,
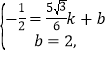
解得:![]() .
.
∴![]()
![]() 存在;
存在;
设![]() 有三种情况;
有三种情况;
当 OD=QD 时,
∵D(0,2),
![]() 即 4m2=22,解得;m=1 或 m=﹣1,
即 4m2=22,解得;m=1 或 m=﹣1,
∴![]()
当 OQ=DQ 时,则![]()
解得:![]()
![]()
当 OD=OQ 时,则 ![]() 解得:m=0,或
解得:m=0,或 ![]()
∴![]()
∴使得三角形 O,D,Q 为等腰三角形的Q 点 Z 坐标为![]()
![]()


科目:初中数学 来源: 题型:
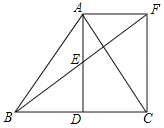
【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
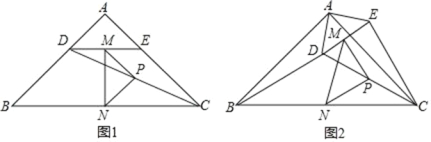
【题目】如图 1,在 Rt△ABC 中,∠A=90°,AB=AC,点 D、E 分别在边 AB、AC 上,AD=AE,连接DC,点 M、P、N 分别为 DE、DC、BC 的中点,
(1)观察猜想:如图 1 中,△PMN 是 三角形;
(2)探究证明:把△ADE 绕点 A 逆时针方向旋转到图 2 的位置,连接 MN,BD, CE.判断△PMN 的形状,并说明理由;
(3)拓展延伸:将△ADE 绕点 A 在平面内自由旋转,若 AD=4,AB=10,请求△PMN 面积的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
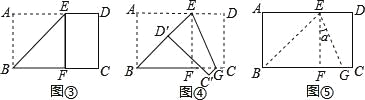
【题目】将长方形纸片 ABCD 沿过点 B 的直线折叠,使点 A 落在 BC 边上的点 F 处, 折痕为 BE(如图③);再沿过点 E 的直线折叠,使点 D 落在 BE 上的点处 D′,折痕为 EG(如图④);再展平纸片(如图⑤),则图⑤中∠α=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇风力资源丰富,为了实现低碳环保,该乡镇决定开展风力发电,打算购买10台风力发电机组.现有A,B两种型号机组,其中A型机组价格为12万元/台,月均发电量为2.4万kw.h;B型机组价格为10万元/台,月均发电量为2万kw.h.经预算该乡镇用于购买风力发电机组的资金不高于105万元.
(1)请你为该乡镇设计几种购买方案;
(2)如果该乡镇用电量不低于20.4万kw.h/月,为了节省资金,应选择那种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①9a﹣3b+c=0;②4a﹣2b+c>0;③方程ax2+bx+c﹣4=0有两个相等的实数根;④方程a(x﹣1)2+b(x﹣1)+c=0的两根是x1=﹣2,x2=2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,交y轴于点E.
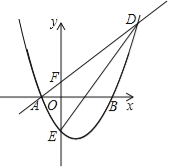
(1)求此抛物线的解析式.
(2)若直线y=x+1与抛物线交于A、D两点,与y轴交于点F,连接DE,求△DEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com