
【题目】将正整数按如图方式进行有规律的排列,第2行最后一个数是4,第3行最后一个数是7,第4行最后一个数是10,…,依此类推,第10行第2个数是__________,第__________行最后一个数是2 020.
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
5 6 7 8 9 10 11 12 13
…
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】长春外国语学校为了创建全省“最美书屋”,购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元.已知学校用12000元购买的科普类图书的本数与用9000元购买的文学类图书的本数相等,求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在梯形ABCD中,AD∥BC,∠ABC=90°,对角线AC、BD相交于点O.下列条件中,不能判断对角线互相垂直的是( ) 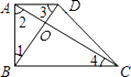
A.∠1=∠4
B.∠1=∠3
C.∠2=∠3
D.OB2+OC2=BC2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A1,A2,A3,A4是数轴上的四个不同点,若|A1A3|=λ|A1A2|,|A1A4|=η|A1A2|,且![]() ,则称A3,A4调和分割A1,A2.已知平面上的点C,D调和分割点A,B,则( )
,则称A3,A4调和分割A1,A2.已知平面上的点C,D调和分割点A,B,则( )
A. 点C可能是线段AB的中点
B. 点C,D可能同时在线段AB上
C. 点D一定不是线段AB的中点
D. 点C,D可能同时在线段AB的延长线上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l1:y=﹣![]() x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.
x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.
(1)求A,B两点的坐标;
(2)求△BOC的面积;
(3)如图2,若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.
①当OA=3MN时,求t的值;
②试探究在坐标平面内是否存在点P,使得以O、Q、C、P为顶点的四边形构成菱形?若存在,请直接写出t的值;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤6,请写出y与x的函数关系式.
(2)若x>6,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料,学校与 图书馆的路程是 ![]() 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线 ![]() 和线段
和线段 ![]() 分别表示两人离学校的路程
分别表示两人离学校的路程 ![]() (千米)与所经过的 时间
(千米)与所经过的 时间 ![]() (分钟)之间的函数关系,请根据图像回答下列问题:
(分钟)之间的函数关系,请根据图像回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟;小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程 ![]() (千米)与所经过的时间
(千米)与所经过的时间 ![]() (分钟)之间的函数表达式;
(分钟)之间的函数表达式;
(3)若设两人在路上相距不超过 ![]() 千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?
千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中.过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做和谐点.例如.图中过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长的数值与面积的数值相等,则点P是和谐点. 
(1)判断点M(1,2),N(4,4)是否为和谐点,并说明理由;
(2)若和谐点P(a,3)在直线y=﹣x+b(b为常数)上,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射线![]() 绕原点
绕原点![]() 从数轴的正半轴逆时针旋转一定的角度
从数轴的正半轴逆时针旋转一定的角度![]() (
(![]() ),射线上的一点
),射线上的一点![]() 与原点
与原点![]() 的距离(
的距离(![]() )为
)为![]() ,并规定:当
,并规定:当![]() 或
或![]() 时,点
时,点![]() 的位置记作
的位置记作![]() ;当
;当![]() 时,点
时,点![]() 的位置记作
的位置记作![]() .如图,点
.如图,点![]() 、
、![]() 的位置表示为
的位置表示为![]() ,
,![]() .回答下列问题:
.回答下列问题:
(1)已知点![]() ,点
,点![]() ,则点
,则点![]() 与点
与点![]() 的距离为 ;线段
的距离为 ;线段![]() 的中点
的中点![]() 的位置是( , ).
的位置是( , ).
(2)已知点![]() ,点
,点![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,以每秒2个单位长度的速度在线段
点出发,以每秒2个单位长度的速度在线段![]() 上来回运动;同时射线
上来回运动;同时射线![]() 以每秒10°的速度绕原点
以每秒10°的速度绕原点![]() 逆时针旋转,当时间
逆时针旋转,当时间![]() (其中
(其中![]() )为何值时,
)为何值时,![]() ?并求出此时三角形
?并求出此时三角形![]() 的面积.
的面积.
(3)直接写出位置满足![]() 的所有点所围成的图形面积.(结果保留一位小数)
的所有点所围成的图形面积.(结果保留一位小数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com