
���� ��1��ֱ�����õ�ƽ�Ƶ����ʵó���Ӧ�����֣�
��2��ֱ�����õ�ƽ�Ƶ����ʵó���Ӧ�����֣�
��3��ֱ�����õ�ƽ�Ƶ����ʵó���Ӧ�����֣�
��4��ֱ�����õ�ƽ�ƵĹ��ɵó���Ӧ�����֣�
��� �⣺��1����A�������ϱ�ʾ+2��A�㿪ʼ�ƶ���
���һ��������ƽ��1����λ��������ƽ��2����λ�����һ���ƶ���������������ϱ�ʾ����Ϊ��2-1+2=3��
��2���ߵڶ����������ƶ�3����λ���������ƶ�4����λ��
��ڶ����ƶ����������������ϱ�ʾ����Ϊ��3-3+4=4��
��3���ߵ������������ƶ�5����λ���������ƶ�6����λ��
��������ƶ���������������ϱ�ʾ����Ϊ��4-5+6=5��
��4�������Ͽɵã���n���ƶ����������������ϱ�ʾ����Ϊ��n+2��
�ʴ�Ϊ����1��+3����2��+4����3��+5����4��2+n��
���� ������Ҫ�����������Լ����ƽ�ƣ���ȷ�ó�ƽ�ƹ����ǽ���ؼ���


 �������ϵ�д�
�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
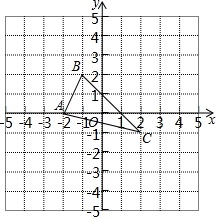 ��ͼ����ƽ��ֱ������ϵ�У���ABC����������������A��-2��0����B��-1��2����C��2��-1������ABC����x��ԳƵ�ͼ���ǡ�A1B1C1��
��ͼ����ƽ��ֱ������ϵ�У���ABC����������������A��-2��0����B��-1��2����C��2��-1������ABC����x��ԳƵ�ͼ���ǡ�A1B1C1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3��27�ĸ��������� | B�� | ��-1��2��ƽ������-1 | ||
| C�� | $\sqrt{64}$����������2 | D�� | ��-1��2����������-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
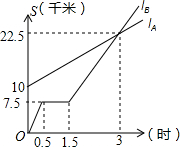 ��ͼ��lA��lB�ֱ��ʾA������B�ﳵ��ͬһ·����ʻ��·��S��ʱ��t�Ĺ�ϵ��
��ͼ��lA��lB�ֱ��ʾA������B�ﳵ��ͬһ·����ʻ��·��S��ʱ��t�Ĺ�ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x-y=y+4}\\{x-y=49+x}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x-y=y+4}\\{x-y=49-x}\end{array}\right.$ | ||
| C�� | $\left\{\begin{array}{l}{x-y=y-4}\\{x-y=49+x}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x-y=y-4}\\{x-y=49-x}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
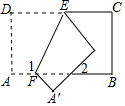 ��ͼ����һ�ų�����ֽƬABCD��EF�۵�������2=40�㣬���1�Ķ���Ϊ��������
��ͼ����һ�ų�����ֽƬABCD��EF�۵�������2=40�㣬���1�Ķ���Ϊ��������| A�� | 110�� | B�� | 115�� | C�� | 125�� | D�� | 130�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | k��3 | B�� | k��3 | C�� | k��3��k��2 | D�� | k��2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com