
已知抛物线经过A(﹣2,0),B(0,2),C(,0)三点,一动点P从原点出发以1个单位/秒的速度沿x轴正方向运动,连接BP,过点A作直线BP的垂线交y轴于点Q.设点P的运动时间为t秒.
(1)求抛物线的解析式;
(2)当BQ=AP时,求t的值;
(3)随着点P的运动,抛物线上是否存在一点M,使△MPQ为等边三角形?若存在,请直接写t的值及相应点M的坐标;若不存在,请说明理由.

解:(1)设抛物线的解析式为y=ax2+bx+c,
∵抛物线经过A(﹣2,0),B(0,2),C(,0)三点,
∴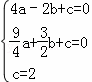 ,
,
解得 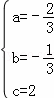 ,
,
∴y=﹣x2﹣x+2.
(2)∵AQ⊥PB,BO⊥AP,
∴∠AOQ=∠BOP=90°,∠PAQ=∠PBO,
∵AO=BO=2,
∴△AOQ≌△BOP,
∴OQ=OP=t.
①如图1,当t≤2时,点Q在点B下方,此时BQ=2﹣t,AP=2+t.
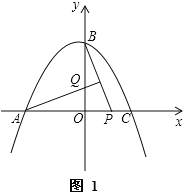
∵BQ=AP,
∴2﹣t=(2+t),
∴t=.
②如图2,当t>2时,点Q在点B上方,此时BQ=t﹣2,AP=2+t.
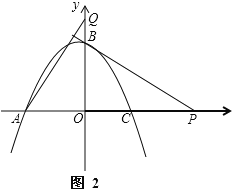
∵BQ=AP,
∴t﹣2=(2+t),
∴t=6.
综上所述,t=或6时,BQ=AP.
(3)当t=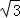 ﹣1时,抛物线上存在点M(1,1);当t=3+3
﹣1时,抛物线上存在点M(1,1);当t=3+3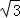 时,抛物线上存在点M(﹣3,﹣3).
时,抛物线上存在点M(﹣3,﹣3).
分析如下:
∵AQ⊥BP,
∴∠QAO+∠BPO=90°,
∵∠QAO+∠AQO=90°,
∴∠AQO=∠BPO.
在△AOQ和△BOP中,
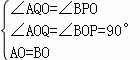 ,
,
∴△AOQ≌△BOP,
∴OP=OQ,
∴△OPQ为等腰直角三角形,
∵△MPQ为等边三角形,则M点必在PQ的垂直平分线上,
∵直线y=x垂直平分PQ,
∴M在y=x上,设M(x,y),
∴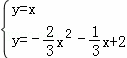 ,
,
解得 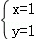 或
或 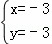 ,
,
∴M点可能为(1,1)或(﹣3,﹣3).
①如图3,当M的坐标为(1,1)时,作MD⊥x轴于D,
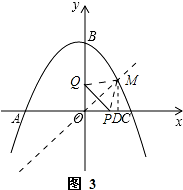
则有PD=|1﹣t|,MP2=1+|1﹣t|2=t2﹣2t+2,PQ2=2t2,
∵△MPQ为等边三角形,
∴MP=PQ,
∴t2+2t﹣2=0,
∴t=﹣1+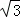 ,t=﹣1﹣
,t=﹣1﹣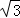 (负值舍去).
(负值舍去).
②如图4,当M的坐标为(﹣3,﹣3)时,作ME⊥x轴于E,
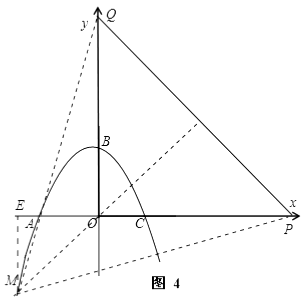
则有PE=3+t,ME=3,
∴MP2=32+(3+t)2=t2+6t+18,PQ2=2t2,
∵△MPQ为等边三角形,
∴MP=PQ,
∴t2﹣6t﹣18=0,
∴t=3+3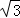 ,t=3﹣3
,t=3﹣3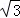 (负值舍去).
(负值舍去).
综上所述,当t=﹣1+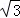 时,抛物线上存在点M(1,1),或当t=3+3
时,抛物线上存在点M(1,1),或当t=3+3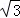 时,抛物线上存在点M(﹣3,﹣3),使得△MPQ为等边三角形.
时,抛物线上存在点M(﹣3,﹣3),使得△MPQ为等边三角形.


 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
如图,一段抛物线y=﹣x(x﹣1)(0≤x≤1)记为m1,它与x轴交点为O、A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3,…,如此进行下去,直至得m10,顶点为P10,则P10的 坐标为( ).
坐标为( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
二次函数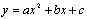 的图象如图l-2-31所示,则下列结论成立的是( )
的图象如图l-2-31所示,则下列结论成立的是( )
A.a>0,bc>0,△<0 B.a<0,bc>0,△<0
C.a>0,bc<0,△<0 D.a<0,bc<0,△>0

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com