
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
Θ®1Θ©Βψ![]() ¥”Βψ
¥”Βψ![]() ΩΣ Φ―Ί
ΩΣ Φ―Ί![]() ±Ώœρ
±Ώœρ![]() “‘
“‘![]() ΒΡΥΌΕ»“ΤΕ·Θ§Βψ
ΒΡΥΌΕ»“ΤΕ·Θ§Βψ![]() ¥”
¥”![]() ΒψΩΣ Φ―Ί
ΒψΩΣ Φ―Ί![]() ±ΏœρΒψ
±ΏœρΒψ![]() “‘
“‘![]() ΒΡΥΌΕ»“ΤΕ·.»γΙϊΒψ
ΒΡΥΌΕ»“ΤΕ·.»γΙϊΒψ![]() Θ§
Θ§![]() Ζ÷±π¥”
Ζ÷±π¥”![]() Θ§
Θ§![]() Ά§ ±≥ωΖΔΘ§Ψ≠ΙΐΦΗΟκΘ§
Ά§ ±≥ωΖΔΘ§Ψ≠ΙΐΦΗΟκΘ§![]() ΒΡΟφΜΐΒ»”Ύ
ΒΡΟφΜΐΒ»”Ύ![]() ΘΩ
ΘΩ
Θ®2Θ©Βψ![]() ¥”Βψ
¥”Βψ![]() ΩΣ Φ―Ί
ΩΣ Φ―Ί![]() ±ΏœρΒψ
±ΏœρΒψ![]() “‘
“‘![]() ΒΡΥΌΕ»“ΤΕ·Θ§Βψ
ΒΡΥΌΕ»“ΤΕ·Θ§Βψ![]() ¥”
¥”![]() ΒψΩΣ Φ―Ί
ΒψΩΣ Φ―Ί![]() ±ΏœρΒψ
±ΏœρΒψ![]() “‘
“‘![]() ΒΡΥΌΕ»“ΤΕ·.»γΙϊΒψ
ΒΡΥΌΕ»“ΤΕ·.»γΙϊΒψ![]() Θ§
Θ§![]() Ζ÷±π¥”
Ζ÷±π¥”![]() Θ§
Θ§![]() Ά§ ±≥ωΖΔΘ§œΏΕΈ
Ά§ ±≥ωΖΔΘ§œΏΕΈ![]() ΡήΖώΫΪ
ΡήΖώΫΪ![]() Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷ΘΩ»τΡήΘ§«σ≥ω‘ΥΕ· ±ΦδΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”….
Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷ΘΩ»τΡήΘ§«σ≥ω‘ΥΕ· ±ΦδΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”….
Θ®3Θ©»τΒψ![]() ―ΊœΏΕΈ
―ΊœΏΕΈ![]() ΖΫœρ¥”
ΖΫœρ¥”![]() Βψ≥ωΖΔ“‘
Βψ≥ωΖΔ“‘![]() ΒΡΥΌΕ»œρΒψ
ΒΡΥΌΕ»œρΒψ![]() “ΤΕ·Θ§Βψ
“ΤΕ·Θ§Βψ![]() ―Ί…δœΏ
―Ί…δœΏ![]() ΖΫœρ¥”
ΖΫœρ¥”![]() Βψ≥ωΖΔ“‘
Βψ≥ωΖΔ“‘![]() ΒΡΥΌΕ»“ΤΕ·Θ§
ΒΡΥΌΕ»“ΤΕ·Θ§![]() Θ§
Θ§![]() Ά§ ±≥ωΖΔΘ§Έ ΦΗΟκΚσΘ§
Ά§ ±≥ωΖΔΘ§Έ ΦΗΟκΚσΘ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() ΘΩ
ΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©2ΟκΜρ4Οκ Θ®2Θ©¥πΑΗΦϊΫβΈω Θ®3Θ©![]() ΟκΜρ5Οκ
ΟκΜρ5Οκ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί÷±Ϋ«»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΚΆ¬Ζ≥Χ=ΥΌΕ»ΓΝ ±ΦδΫχ––«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©…ηΨ≠Ιΐ![]() ΟκΘ§œΏΕΈ
ΟκΘ§œΏΕΈ![]() ΡήΖώΫΪ
ΡήΖώΫΪ![]() Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷Θ§ΗυΨίΟφΜΐ÷°ΦδΒΡΒ»ΝΩΙΊœΒΚΆ≈–±π ΫΦ¥Ω…«σΫβΘΜ
Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷Θ§ΗυΨίΟφΜΐ÷°ΦδΒΡΒ»ΝΩΙΊœΒΚΆ≈–±π ΫΦ¥Ω…«σΫβΘΜ
Θ®3Θ©Ζ÷ΝΫ÷÷«ιΩωΘΚΔΌΒ±Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ ±ΘΜ
…œ ±ΘΜ
ΔΎΒ±Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() ΒΡ―”≥ΛœΏ…œ ±Θ§Ϋχ––Χ÷¬έΦ¥Ω…«σΫβ.
ΒΡ―”≥ΛœΏ…œ ±Θ§Ϋχ––Χ÷¬έΦ¥Ω…«σΫβ.
ΫβΘΚΘ®1Θ©…ηΨ≠Ιΐ![]() ΟκΘ§
ΟκΘ§![]() ΒΡΟφΜΐΒ»”Ύ
ΒΡΟφΜΐΒ»”Ύ![]() Θ§“άΧβ“β”–
Θ§“άΧβ“β”–
![]() Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§![]() Θ§
Θ§
Ψ≠Φλ―ιΘ§![]() Θ§
Θ§![]() ΨυΖϊΚœΧβ“β.
ΨυΖϊΚœΧβ“β.
¥πΘΚΨ≠Ιΐ2ΟκΜρ4ΟκΘ§![]() ΒΡΟφΜΐΒ»”Ύ
ΒΡΟφΜΐΒ»”Ύ![]() .
.
Θ®2Θ©…ηΨ≠Ιΐ![]() ΟκΘ§œΏΕΈ
ΟκΘ§œΏΕΈ![]() ΫΪ
ΫΪ![]() Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷“άΧβ“β”–
Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷“άΧβ“β”–
![]() Θ§
Θ§
Μ·ΦρΩ…ΒΟ![]() .
.
ΓΏ![]() .Γύ¥ΥΖΫ≥ΧΈό Β ΐΗυ.
.Γύ¥ΥΖΫ≥ΧΈό Β ΐΗυ.
ΓύœΏΕΈ![]() ≤ΜΡήΫΪ
≤ΜΡήΫΪ![]() Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷.
Ζ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷.
Θ®3Θ©Β±Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ ±Θ§
…œ ±Θ§
…ηΨ≠Ιΐ![]() ΟκΘ§
ΟκΘ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() .
.
“άΧβ“β”–![]() Θ§
Θ§![]()
ΫβΒΟ![]() Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§![]() Θ§
Θ§
Γύ![]() ΘΜ
ΘΜ
Β±Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() ΒΡ―”≥ΛœΏ…œ ±Θ§
ΒΡ―”≥ΛœΏ…œ ±Θ§
…ηΨ≠Ιΐ![]() ΟκΘ§
ΟκΘ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() .
.
“άΧβ“β”–![]() Θ§
Θ§![]() Θ§
Θ§
ΫβΒΟ![]() .
.
Ψ≠Φλ―ιΘ§![]() ΖϊΚœΧβ“β.
ΖϊΚœΧβ“β.
Ήέ…œΥυ ωΘ§Ψ≠Ιΐ![]() ΟκΜρ5ΟκΘ§
ΟκΜρ5ΟκΘ§![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() .
.


 ≥ε¥Χ100Ζ÷1Κ≈ΨμœΒΝ–¥πΑΗ
≥ε¥Χ100Ζ÷1Κ≈ΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ![]() Θ§“‘
Θ§“‘![]() ΈΣ÷±ΨΕΘ§
ΈΣ÷±ΨΕΘ§![]() ΈΣ‘≤–ΡΒΡΑκ‘≤ΫΜ
ΈΣ‘≤–ΡΒΡΑκ‘≤ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() ΈΣΜΓ
ΈΣΜΓ![]() ΒΡ÷–ΒψΘ§Ν§Ϋ”
ΒΡ÷–ΒψΘ§Ν§Ϋ”![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() ΒΡΫ«ΤΫΖ÷œΏΘ§«“
ΒΡΫ«ΤΫΖ÷œΏΘ§«“![]() Θ§¥ΙΉψΈΣΒψ
Θ§¥ΙΉψΈΣΒψ![]() .≈–Εœ÷±œΏ
.≈–Εœ÷±œΏ![]() ”κ
”κ![]() ΒΡΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
ΒΡΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
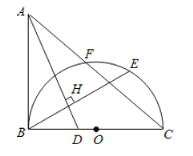
ΓΨΧβΡΩΓΩ»γΆΦΘ§EΘ§FΘ§GΘ§HΖ÷±π «BDΘ§BCΘ§ACΘ§ADΒΡ÷–ΒψΘ§«“AB=CDΘ§œ¬Ν–Ϋα¬έΘΚΔΌEGΓΆFHΘΜΔΎΥΡ±Ώ–ΈEFGH «Νβ–ΈΘΜΔέHFΤΫΖ÷ΓœEHGΘΜΔήEG=![]() Θ®BC©¹ADΘ©Θ§Τδ÷–’ΐ»ΖΒΡΗω ΐ «Θ®ΓΓΓΓΘ©
Θ®BC©¹ADΘ©Θ§Τδ÷–’ΐ»ΖΒΡΗω ΐ «Θ®ΓΓΓΓΘ©

A. 1Ηω B. 2Ηω C. 3Ηω D. 4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
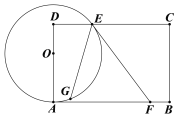
ΓΨΧβΡΩΓΩ»γΆΦΘ§OΈΣΨΊ–ΈABCD±ΏAD…œ“ΜΒψΘ§“‘OΈΣ‘≤–ΡΘ§OAΈΣΑκΨΕΜ≠‘≤”κCDΫΜ”ΎΒψEΘ§ΙΐΒψEΉςΓ―OΒΡ«–œΏEFΫΜAB”ΎFΘ§ΒψCΙΊ”ΎEFΒΡΕ‘≥ΤΒψG«ΓΚΟ¬δ‘ΎΓ―O…œΘ§»τAD=4,AB=6,‘ρOAΒΡ≥ΛΈΣ____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœΰΕΪ‘ΎΫβ“Μ‘ΣΕΰ¥ΈΖΫ≥Χ ±Θ§ΖΔœ÷”–’β―υ“Μ÷÷ΫβΖ®ΘΚ
»γΘΚΫβΖΫ≥Χ![]() .
.
ΫβΘΚ‘≠ΖΫ≥ΧΩ…±δ–ΈΘ§ΒΟ
![]() .
.
![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
÷±Ϋ”ΩΣΤΫΖΫ≤Δ’ϊάμΘ§ΒΟ![]() Θ§
Θ§![]() .
.
Έ“Ο«≥ΤœΰΕΪ’β÷÷ΫβΖ®ΈΣΓΑΤΫΨυ ΐΖ®Γ±Θ°
Θ®1Θ©œ¬Οφ «œΰΕΪ”ΟΓΑΤΫΨυ ΐΖ®Γ±ΫβΖΫ≥Χ![]() ±–¥ΒΡΫβΧβΙΐ≥ΧΘ°
±–¥ΒΡΫβΧβΙΐ≥ΧΘ°
![]() .
.
![]() Θ§
Θ§
![]() .
.
÷±Ϋ”ΩΣΤΫΖΫ≤Δ’ϊάμΘ§ΒΟ![]() Θ§
Θ§![]() .
.
…œ ωΙΐ≥Χ÷–ΒΡΓΑΓθΓ±Θ§ΓΑΓπΓ±Θ§ΓΑΓνΓ±Θ§ΓΑΓηΓ±±μ ΨΒΡ ΐΖ÷±πΈΣ________Θ§________Θ§________Θ§________.
Θ®2Θ©«κ”ΟΓΑΤΫΨυ ΐΖ®Γ±ΫβΖΫ≥ΧΘΚ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
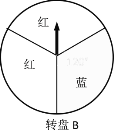
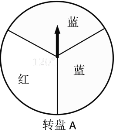
ΓΨΧβΡΩΓΩΡ≥…Χ≥Γ‘Ύ¥ΌœζΜνΕ·÷–ΙφΕ®Θ§ΙΥΩΆΟΩœϊΖ―100‘ΣΨΆΡήΜώΒΟ“Μ¥Έ≥ιΫ±ΜζΜαΘ°ΈΣΝΥΜν‘ΨΤχΖ’Θ§…ηΦΤΝΥΝΫΗω≥ιΫ±ΖΫΑΗΘΚ
ΖΫΑΗ“ΜΘΚΉΣΕ·ΉΣ≈ΧA“Μ¥ΈΘ§ΉΣ≥ωΚλ…ΪΩ…Νλ»Γ“ΜΖίΫ±ΤΖΘΜ
ΖΫΑΗΕΰΘΚΉΣΕ·ΉΣ≈ΧBΝΫ¥ΈΘ§ΝΫ¥ΈΕΦΉΣ≥ωΚλ…ΪΩ…Νλ»Γ“ΜΖίΫ±ΤΖΘ°Θ®ΝΫΗωΉΣ≈ΧΕΦ±ΜΤΫΨυΖ÷≥…3ΖίΘ©»γΙϊΡψΜώΒΟ“Μ¥Έ≥ιΫ±ΜζΜαΘ§ΡψΜα―Γ‘ώΡΡΗωΖΫΑΗΘΩ«κ”ΟœύΙΊΒΡ ΐ―ß÷Σ ΕΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
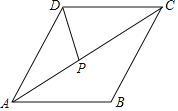
ΓΨΧβΡΩΓΩ»γΆΦΘ§Νβ–ΈABCDΒΡ±Ώ≥ΛΈΣ4Θ§ΓœBΘΫ120ΓψΘ°ΒψP «Ε‘Ϋ«œΏAC…œ“ΜΒψΘ®≤Μ”κΕΥΒψA÷ΊΚœΘ©Θ§‘ρœΏΕΈ![]() AP+PDΒΡΉν–Γ÷ΒΈΣ_____Θ°
AP+PDΒΡΉν–Γ÷ΒΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
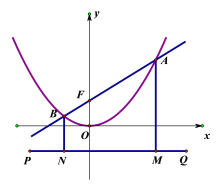
ΓΨΧβΡΩΓΩ“―÷Σ÷±œΏlΘΚy=kx+4”κ≈ΉΈοœΏy=![]() x2ΫΜ”ΎΒψA(x1Θ§y1)Θ§B(x2Θ§y2)Θ°
x2ΫΜ”ΎΒψA(x1Θ§y1)Θ§B(x2Θ§y2)Θ°
(1)«σΘΚ![]() ΘΜ
ΘΜ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
(2)ΙΐΒψ(0Θ§-4)Ής÷±œΏPQΓΈx÷αΘ§«“ΙΐΒψAΓΔBΖ÷±πΉςAMΓΆPQ”ΎΒψMΘ§BNΓΆPQ”ΎΒψNΘ§…η÷±œΏlΘΚy=kx+4ΫΜy÷α”ΎΒψFΘ°«σ÷ΛΘΚAF=AM=4+y1Θ°
(3)÷ΛΟςΘΚ![]() +
+![]() ΈΣΕ®÷ΒΘ§≤Δ«σ≥ωΗΟ÷ΒΘ°
ΈΣΕ®÷ΒΘ§≤Δ«σ≥ωΗΟ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
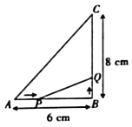
ΓΨΧβΡΩΓΩ»γΆΦΘ§RtΓςABC÷–Θ§ΓœC=90ΓψΘ§AB=4![]() Θ§F «œΏΕΈAC…œ“ΜΒψΘ§ΙΐΒψAΒΡΓ―FΫΜAB”ΎΒψDΘ§E «œΏΕΈBC…œ“ΜΒψΘ§«“ED=EBΘ§‘ρEFΒΡΉν–Γ÷ΒΈΣ Θ® Θ©
Θ§F «œΏΕΈAC…œ“ΜΒψΘ§ΙΐΒψAΒΡΓ―FΫΜAB”ΎΒψDΘ§E «œΏΕΈBC…œ“ΜΒψΘ§«“ED=EBΘ§‘ρEFΒΡΉν–Γ÷ΒΈΣ Θ® Θ©

A. 3![]() B. 2
B. 2![]() C.
C. ![]() D. 2
D. 2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com