
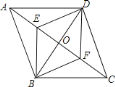
【题目】如图,![]() 是菱形
是菱形![]() 的对角线
的对角线![]() 、
、![]() 的交点,
的交点,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.下列结论:①
的中点.下列结论:①![]() ;②四边形
;②四边形![]() 也是菱形;③四边形
也是菱形;③四边形![]() 的面积为
的面积为![]() ;④
;④![]() ;⑤
;⑤![]() 是轴对称图形.其中正确的结论有( )
是轴对称图形.其中正确的结论有( )
A. 5个 B. 4个 C. 3个 D. 2个
【答案】B
【解析】
①正确,根据三角形的面积公式可得到结论;②根据已知条件利用菱形的判定定理可证得其正确;③正确,根据菱形的面积等于对角线乘积的一半即可求得;④不正确,根据已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO;⑤正确,由已知可证得△DEO≌△DFO,从而可推出结论正确.
①正确
∵E、F分别是OA、OC的中点.
∴AE=OE.
∵S![]() .
.
∴![]() .
.
②正确
∵四边形ABCD是菱形,E,F分别是OA,OC的中点.
∴EF⊥OD,OE=OF,
∵OD=OD.
∴DE=DF.
同理:BE=BF
∴四边形BFDE是菱形.
③正确
∵菱形ABCD的面积=![]() AC×BD.
AC×BD.
∵E、F分别是OA、OC的中点.
∴EF=![]() AC.
AC.
∴菱形ABCD的面积=EF×BD.
④不正确
由已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.
⑤正确
∵EF⊥OD,OE=OF,OD=OD.
∴△DEO≌△DFO.
∴△DEF是轴对称图形.
∴正确的结论有四个,分别是①②③⑤,故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
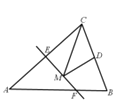
【题目】如图,等腰三角形ABC的底边BC长为6,面积是36,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() 、
、![]() 为对角线,点
为对角线,点![]() 、
、![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 、
、![]() 边的中点,下列说法:
边的中点,下列说法:
①当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.
四点共圆.
②当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.
四点共圆.
③当![]() 且
且![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.
四点共圆.
其中正确的是( )

A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知点A(-1,4),B(-2,2),C(1,1).

(1)作ΔABC关于x轴对称的△A1B1C1,并写出点A1,B1,C1的坐标,
(2)作△ABC关于y轴对称的△A2B2C2,并写出点A2,B2,C2的坐标,
(3)观察点A1,B1,C1和A2,B2,C2的坐标,请用文字语言归纳点A1和A2,B1和B2,C1和C2坐标之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将两个全等的三角板如图摆放,其中△ABC和ΔADE的直角顶点重合在点A处,∠ADE=∠ABC=60°,且点D在AC上,点B在AE上,∠C=∠E=30°,AB=AD,AC=AE,BC=DE,BC和DE相交于点F.求证:CF=EF.

(2)如图2,将这两个三角板如图摆放,直角顶点A仍然重合,BC与DE相交于点F,AC与DE交于点M,AE和BC交于点N.猜想CF和EF还相等吗?说明理由.
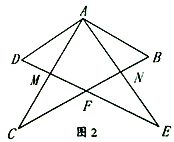
(3)如图3,在(2)的基础上,若∠DAM=30°.求证:线段DF和AC互相垂直平分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() ,在不再连接其他线段的前提下,要使四边形
,在不再连接其他线段的前提下,要使四边形![]() 成为菱形,还需添加一个条件,这个条件不可能是( )
成为菱形,还需添加一个条件,这个条件不可能是( )

A. BD=DC B. AB=AC
C. AD=BC D. AD⊥BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com