
【题目】如图,正方形![]() 的边长是4,
的边长是4,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,若点
,若点![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,则
上的动点,则![]() 的最小值是__________.
的最小值是__________.

【答案】![]()
【解析】
过![]() 作
作![]() 的垂线交
的垂线交![]() 于F,交AC于D′,再过D′作D′P′⊥AD,由角平分线的性质可得出D′是D关于AE的对称点,进而可知D′P′即为DQ+PQ的最小值.
于F,交AC于D′,再过D′作D′P′⊥AD,由角平分线的性质可得出D′是D关于AE的对称点,进而可知D′P′即为DQ+PQ的最小值.
解:过![]() 作
作![]() 的垂线交
的垂线交![]() 于F,交AC于D′,再过D′作D′P′⊥AD,如下图,
于F,交AC于D′,再过D′作D′P′⊥AD,如下图,
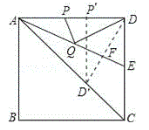
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=4,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=16,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=16,
∴P′D′=![]() ,
,
即![]() 的最小值是
的最小值是![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②4a+2b+c<0;③a﹣b+c>0;④(a+c)2<b2 . 其中正确的结论是( )
A.①②
B.①③
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:
①c>0;
②若点B(﹣ ![]() ,y1)、C(﹣
,y1)、C(﹣ ![]() ,y2)为函数图象上的两点,则y1<y2;
,y2)为函数图象上的两点,则y1<y2;
③2a﹣b=0;
④ ![]() <0,
<0,
其中,正确结论的个数是( )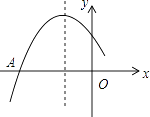
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ACB,∠ACB=90°,AC=BC,点A、C分别在x轴、y轴的正半轴上.

(1)如图1,求证:∠BCO=∠CAO
(2)如图2,若OA=5,OC=2,求B点的坐标
(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=18.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,OP的长度是否发生改变?若不变,求出OP的值;若变化,求OP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD在平面直角坐标系中,AD∥BC∥x轴,AB∥DC∥y轴,x轴与y轴夹角为90°,点M,N分别在xy轴上,点A(1,8),B(1,6),C(7,6),D(7,8).

(1)连接线段OB、OD、BD,求△OBD的面积;
(2)若长方形ABCD在第一象限内以每秒0.5个单位长度的速度向下平移,经过多少秒时,△OBD的面积与长方形ABCD的面积相等请直接写出答案;
(3)见备用图,连接 OB,OD,OD交BC于点E,∠BON的平分线和∠BEO的平分线交于点F.
①当∠BEO的度数为n,∠BON的度数为m时,求∠OFE的度数.
②请直接写出∠OFE和∠BOE之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:把形如![]() 的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即
的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即![]() .例如:
.例如:![]()
![]() 是
是![]() 的一种形式的配方;所以,
的一种形式的配方;所以,![]() ,
,![]()
![]() ,
,![]() 是
是![]() 的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).
的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).
请根据阅读材料解决下列问题:
(1)比照上面的例子,写出![]() 三种不同形式的配方;
三种不同形式的配方;
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上一点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.
(1)求证:四边形CDEF是菱形.
(2)当∠ACB= 度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知一次函数y=ax+2与x轴、y轴分别交于点A,B,反比例函数y= ![]() 经过点M.
经过点M.
(1)若M是线段AB上的一个动点(不与点A、B重合).当a=﹣3时,设点M的横坐标为m,求k与m之间的函数关系式.
(2)当一次函数y=ax+2的图象与反比例函数y= ![]() 的图象有唯一公共点M,且OM=
的图象有唯一公共点M,且OM= ![]() ,求a的值.
,求a的值.
(3)当a=﹣2时,将Rt△AOB在第一象限内沿直线y=x平移 ![]() 个单位长度得到Rt△A′O′B′,如图2,M是Rt△A′O′B′斜边上的一个动点,求k的取值范围.
个单位长度得到Rt△A′O′B′,如图2,M是Rt△A′O′B′斜边上的一个动点,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com