
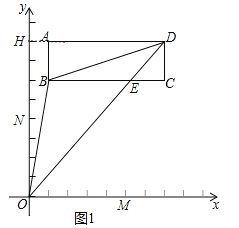
°æƒø°ø»ÁÕº£¨≥§∑Ω–ŒABCD‘Ğ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨AD°ŒBC°Œx÷·£¨AB°ŒDC°Œy÷·£¨x÷·”Îy÷·º–Ω«Œ™90°„£¨µ„M£¨N∑÷±‘Ğxy÷·…œ£¨µ„A£®1£¨8£©£¨B£®1£¨6£©£¨C£®7£¨6£©£¨D£®7£¨8£©£Æ

£®1£©¡¨Ω”œş∂ŒOB°¢OD°¢BD£¨«Û°˜OBDµƒ√ʪ˝£ª
£®2£©»Ù≥§∑Ω–ŒABCD‘еГªœÛœŞƒĞ“‘√ø√Î0.5∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚœ¬∆Ω“∆£¨æ≠π˝∂‡…Ÿ√Î ±£¨°˜OBDµƒ√ʪ˝”Î≥§∑Ω–ŒABCDµƒ√ʪ˝œ‡µ»«Î÷±Ω”–¥≥ˆ¥∞∏£ª
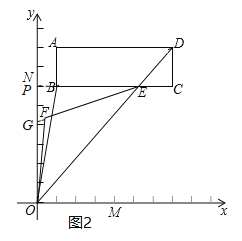
£®3£©º˚±∏”√Õº£¨¡¨Ω” OB£¨OD£¨ODΩªBC”е„E£¨°œBONµƒ∆Ω∑÷œş∫Õ°œBEOµƒ∆Ω∑÷œşΩª”е„F£Æ
¢Ÿµ±°œBEOµƒ∂» ˝Œ™n£¨°œBONµƒ∂» ˝Œ™m ±£¨«Û°œOFEµƒ∂» ˝£Æ
¢Ğ«Î÷±Ω”–¥≥ˆ°œOFE∫Õ°œBOE÷ƺ‰µƒ ˝¡øπÿœµ£Æ
°æ¥∞∏°ø£®1£©17£ª£®2£©![]() £ª£®3£©¢Ÿ°œEFO£Ω
£ª£®3£©¢Ÿ°œEFO£Ω![]() m+
m+![]() n+90°„£ª¢Ğ2°œEFO+°œBOE£Ω270°„£Æ
n+90°„£ª¢Ğ2°œEFO+°œBOE£Ω270°„£Æ
°æΩ‚Œˆ°ø
£®1£©—”≥§DAΩªy÷·”ĞH£¨»ÁÕº1À˘ 棨‘ÚAH°Õy÷·£¨»ª∫Û¿˚”√S°˜OBD£ΩS°˜ODH©ÅS°˜ABD©ÅSÃı–ŒAHOB¥˙»Î ˝æıº∆À„º¥ø…£ª
£®2£©”…S°˜OBD£ΩS°˜ODH©ÅS°˜ABD©ÅSÃı–ŒAHOB£ΩS≥§∑Ω–ŒABCD£Ω12º¥ø…¡–≥ˆπÿ”Ğtµƒ∑Ω≥ã¨Ω‚∑Ω≥ú¥µ√Ω·π˚£ª
£®3£©¢Ÿ—”≥§CBΩªy÷·”е„P£¨—”≥§EFΩªy÷·”е„G£¨»ÁÕº2£¨∏˘æıΩ«∆Ω∑÷œşµƒ∂®“Â∫Õ»˝Ω«–ŒµƒÕ‚Ω«–‘÷ Ω‚¥º¥ø…£ª
¢Ğ∏˘æıΩ«∆Ω∑÷œşµƒ∂®“Â∫Õ»˝Ω«–ŒµƒÕ‚Ω«–‘÷ ø…µ√°œEFO£Ω90°„+![]() (°œNOB+°œBEO)£¨∏˘æı÷±Ω«»˝Ω«–Œµƒ–‘÷ ø…µ√°œBON+°œBEO=90°„£≠°œBOE£¨Ω¯“ª≤Ωº¥ø…µ√≥ˆΩ·¬ğ£Æ
(°œNOB+°œBEO)£¨∏˘æı÷±Ω«»˝Ω«–Œµƒ–‘÷ ø…µ√°œBON+°œBEO=90°„£≠°œBOE£¨Ω¯“ª≤Ωº¥ø…µ√≥ˆΩ·¬ğ£Æ
Ω‚£∫£®1£©—”≥§DAΩªy÷·”ĞH£¨»ÁÕº1À˘ æ£∫
‘ÚAH°Õy÷·£Æ
°şA£®1£¨8£©£¨B£®1£¨6£©£¨C£®7£¨6£©£¨D£®7£¨8£©
°‡OH£Ω8£¨DH£Ω7£¨AH£Ω1£¨AD£Ω6£¨AB£Ω2£¨
°‡S°˜OBD£ΩS°˜ODH©ÅS°˜ABD©ÅSÃı–ŒAHOB
£Ω![]() °¡OH°¡DH©Å
°¡OH°¡DH©Å![]() °¡AB°¡AD©Å
°¡AB°¡AD©Å![]() °¡£®AB+OH£©°¡AH
°¡£®AB+OH£©°¡AH
£Ω![]() °¡8°¡7©Å
°¡8°¡7©Å![]() °¡2°¡6©Å
°¡2°¡6©Å![]() °¡£®2+8£©°¡1£Ω17£ª
°¡£®2+8£©°¡1£Ω17£ª
£®2£©°şS≥§∑Ω–ŒABCD£Ω2°¡6£Ω12£¨
°‡S°˜OBD£ΩS°˜ODH©ÅS°˜ABD©ÅSÃı–ŒAHOB£Ω12£¨
°‡![]() °¡£®8©Å0.5t£©°¡7©Å
°¡£®8©Å0.5t£©°¡7©Å![]() °¡2°¡6©Å
°¡2°¡6©Å![]() °¡£®2+8©Å0.5t£©°¡1£Ω12£¨
°¡£®2+8©Å0.5t£©°¡1£Ω12£¨
Ω‚µ√£∫t£Ω![]() £ª
£ª
£®3£©¢Ÿ—”≥§CBΩªy÷·”е„P£¨—”≥§EFΩªy÷·”е„G£¨»ÁÕº2£¨
°şEF∆Ω∑÷°œBEO£¨OF∆Ω∑÷°œNOB£¨
°‡°œGOF£Ω![]() °œNOB£Ω
°œNOB£Ω![]() m£¨°œBEF£Ω
m£¨°œBEF£Ω![]() °œBEO£Ω
°œBEO£Ω![]() n£¨
n£¨
°ş°œEFO£Ω°œGOF+°œFGO£¨°œFGO£Ω°œGPE+°œBEF£¨
°‡°œEFO£Ω°œGOF+°œGPE+°œBEF£Ω![]() m+
m+![]() n+90°„£ª
n+90°„£ª
¢Ğ°şEF∆Ω∑÷°œBEO£¨OF∆Ω∑÷°œNOB£¨
°‡°œGOF£Ω![]() °œNOB£¨°œBEF£Ω
°œNOB£¨°œBEF£Ω![]() °œBEO£¨
°œBEO£¨
°ş°œEFO£Ω°œGOF+°œFGO£¨°œFGO£Ω°œGPE+°œBEF£¨
°‡°œEFO£Ω°œGOF+°œGPE+°œBEF£Ω90°„+![]() °œNOB+
°œNOB+![]() °œBEO£Ω90°„+
°œBEO£Ω90°„+![]() (°œNOB+°œBEO)£¨
(°œNOB+°œBEO)£¨
°ş°œBOE£Ω90°„©Å°œBON©Å°œBEO£¨
°‡°œBON+°œBEO=90°„£≠°œBOE£¨
°‡°œEFO£Ω90°„+![]() (90°„£≠°œBOE)£¨
(90°„£≠°œBOE)£¨
º¥2°œEFO+°œBOE£Ω270°„£Æ



| ƒÍº∂ | ∏ş÷–øŒ≥à | ƒÍº∂ | ≥÷–øŒ≥à |
| ∏ş“ª | ∏ş“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥“ª | ≥“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş∂˛ | ∏ş∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥∂˛ | ≥∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş»˝ | ∏ş»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥»˝ | ≥»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ“œÿÕÚµ¬¬°…Ã≥°”–A°¢B¡Ω÷÷…Ã∆∑µƒΩ¯ºğ∫Õ ğºğ»Á±Ì£∫
…Ã∆∑ ºğ∏Ò | A | B |
Ω¯ºğ£®‘™/º˛£© | m | m+20 |
ğºğ£®‘™/º˛£© | 160 | 240 |
“—÷™£∫”√2400‘™π∫Ω¯A÷÷…Ã∆∑µƒ ˝¡ø”Δ√3000‘™π∫Ω¯B÷÷…Ã∆∑µƒ ˝¡øœ‡Õ¨£Æ
£®1£©«Ûmµƒ÷µ£ª
£®2£©∏√…Ã≥°º∆ªÆÕ¨ ±π∫Ω¯µƒA°¢B¡Ω÷÷…Ã∆∑π≤200º˛£¨∆‰÷–π∫Ω¯A÷÷…Ã∆∑xº˛£¨ µº Ω¯ª ±£¨…˙≤˙≥ߺ“∂‘A÷÷…Ã∆∑µƒ≥ˆ≥ߺ𜬵˜a£®50£ºa£º70£©‘™≥ˆ 𣨻مÃ≥°±£≥÷Õ¨÷÷…Ã∆∑µƒ ğºğ≤ª±‰£¨…Ã≥° ğÕÍ’‚200º˛…Ã∆∑µƒ◊İ¿˚»ÛŒ™y‘™£Æ
¢Ÿ«Ûyπÿ”Ğxµƒ∫Ø ˝πÿœµ Ω£ª
¢Ğ»ÙœŞ∂®A÷÷…Ã∆∑◊Ó∂‡π∫Ω¯120º˛◊Ó…Ÿπ∫Ω¯100º˛£¨«Îƒ„∏˘æı“‘…œ–≈œ¢£¨…˺∆≥ˆ π∏√…Ã≥°ªÒµ√◊Ó¥Û¿˚»ÛµƒΩ¯ª∑Ω∞∏£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨![]() √ʪ˝Œ™
√ʪ˝Œ™![]() £¨µĞ“ª¥Œ≤Ÿ◊˜£∫∑÷±—”≥§
£¨µĞ“ª¥Œ≤Ÿ◊˜£∫∑÷±—”≥§![]() ÷¡µ„
÷¡µ„![]() π
π![]() £¨À≥¥Œ¡¨Ω·
£¨À≥¥Œ¡¨Ω·![]() £¨µ√µΩ
£¨µ√µΩ![]() £¨µĞ∂˛¥Œ≤Ÿ◊˜£∫∑÷±—”≥§
£¨µĞ∂˛¥Œ≤Ÿ◊˜£∫∑÷±—”≥§![]() ÷¡µ„
÷¡µ„![]() £¨ π
£¨ π![]() £¨À≥¥Œ¡¨Ω·
£¨À≥¥Œ¡¨Ω·![]() £¨µ√µΩ
£¨µ√µΩ![]() £¨ £Æ£Æ∞¥¥Àπʬ…£¨“™ πµ√µΩµƒ»˝Ω«–Œµƒ√ʪ˝≥¨π˝
£¨ £Æ£Æ∞¥¥Àπʬ…£¨“™ πµ√µΩµƒ»˝Ω«–Œµƒ√ʪ˝≥¨π˝![]() £¨÷¡…Ÿæ≠π˝_________¥Œ≤Ÿ◊˜£Æ
£¨÷¡…Ÿæ≠π˝_________¥Œ≤Ÿ◊˜£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘Ğæÿ–ŒABCD÷–£¨AB=2£¨AD=5£¨π˝µ„A°¢B◊˜°—O£¨ΩªAD£¨BC”е„E£¨F£¨¡¨Ω”BE£¨CE£¨π˝µ„F◊˜FG°ÕCE£¨¥π◊„Œ™G£Æ
£®1£©µ±µ„F «BCµƒ÷–µ„ ±£¨«Û÷§£∫÷±œşFG”ΰ—Oœ‡«–£ª
£®2£©»ÙFG°ŒBE ±£¨«ÛAEµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨’˝∑Ω–Œ![]() µƒ±ş≥§ «4£¨
µƒ±ş≥§ «4£¨![]() µƒ∆Ω∑÷œşΩª
µƒ∆Ω∑÷œşΩª![]() ”е„
”е„![]() £¨»Ùµ„
£¨»Ùµ„![]() °¢
°¢![]() ∑÷± «
∑÷± «![]() ∫Õ
∫Õ![]() …œµƒ∂ص„£¨‘Ú
…œµƒ∂ص„£¨‘Ú![]() µƒ◊Ó–°÷µ «__________£Æ
µƒ◊Ó–°÷µ «__________£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕº£¨![]() £¨M «BCµƒ÷–µ„£¨DM∆Ω∑÷
£¨M «BCµƒ÷–µ„£¨DM∆Ω∑÷![]() £Æ
£Æ

£®1£©«Û÷§£∫AM∆Ω∑÷![]() £ª
£ª
£®2£©œş∂ŒDM”ÎAM”–‘—˘µƒŒª÷√πÿœµ£ø«ÎÀµ√˜¿Ì”…£ª
£®3£©œş∂ŒCD°¢AB°¢ADº‰”–‘—˘µƒ ˝¡øπÿœµ£ø«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø¿˚”√Œ“√«—ßπ˝µƒ÷™ ∂£¨ø…“‘µ√≥ˆœ¬√Ê’‚∏ˆ”≈√¿µƒµ» Ω£∫
![]() £ª∏√µ» Ω¥”◊ÛµΩ”“µƒ±‰–Œ£¨≤ªΩˆ±£≥÷¡ÀΩ·ππµƒ∂‘≥∆–‘£¨ªπÃÂœ÷¡À ˝—ßµƒ∫Õ–≥°¢ºÚΩ‡√¿.
£ª∏√µ» Ω¥”◊ÛµΩ”“µƒ±‰–Œ£¨≤ªΩˆ±£≥÷¡ÀΩ·ππµƒ∂‘≥∆–‘£¨ªπÃÂœ÷¡À ˝—ßµƒ∫Õ–≥°¢ºÚΩ‡√¿.
¢≈.«Îƒ„÷§√˜’‚∏ˆµ» Ω£ª
¢∆.»Áπ˚![]() £¨«Îƒ„«Û≥ˆ
£¨«Îƒ„«Û≥ˆ ![]() µƒ÷µ.
µƒ÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨ƒ≥»À‘Ğ…Ω∆¬∆¬Ω≈A¥¶≤‚µ√µÁ ”À˛º‚µ„Cµƒ—ˆΩ«Œ™60°„£¨—ÿ…Ω∆¬œÚ…œ◊şµΩP¥¶‘Ÿ≤‚µ√Cµƒ—ˆΩ«Œ™45°„£¨“—÷™OA=200√◊£¨…Ω∆¬∆¬∂»Œ™ ![]() £®º¥tan°œPAB=
£®º¥tan°œPAB= ![]() £©£¨«“O£¨A£¨B‘ĞÕ¨“ªÃ÷±œş…œ£¨«ÛµÁ ”À˛OCµƒ∏ş∂»“‘º∞¥À»ÀÀ˘‘еƒŒª÷√µ„Pµƒ¥π÷±∏ş∂»£Æ£®≤‡«„∆˜µƒ∏ş∂»∫ˆ¬‘≤ªº∆£¨Ω·π˚±£¡Ù∏˘∫≈£©
£©£¨«“O£¨A£¨B‘ĞÕ¨“ªÃ÷±œş…œ£¨«ÛµÁ ”À˛OCµƒ∏ş∂»“‘º∞¥À»ÀÀ˘‘еƒŒª÷√µ„Pµƒ¥π÷±∏ş∂»£Æ£®≤‡«„∆˜µƒ∏ş∂»∫ˆ¬‘≤ªº∆£¨Ω·π˚±£¡Ù∏˘∫≈£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨AB «°—Oµƒ÷±æ∂£¨C£¨D «°—O…œµƒµ„£¨°œCDB=20°„£¨π˝µ„C◊˜°—Oµƒ«–œşΩªABµƒ—”≥§œş”е„E£¨‘Ú°œE= £Æ 
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒŞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com