
【题目】我县万德隆商场有A、B两种商品的进价和售价如表:
商品 价格 | A | B |
进价(元/件) | m | m+20 |
售价(元/件) | 160 | 240 |
已知:用2400元购进A种商品的数量与用3000元购进B种商品的数量相同.
(1)求m的值;
(2)该商场计划同时购进的A、B两种商品共200件,其中购进A种商品x件,实际进货时,生产厂家对A种商品的出厂价下调a(50<a<70)元出售,若商场保持同种商品的售价不变,商场售完这200件商品的总利润为y元.
①求y关于x的函数关系式;
②若限定A种商品最多购进120件最少购进100件,请你根据以上信息,设计出使该商场获得最大利润的进货方案.
【答案】(1)80;(2)①y=(a﹣60)x+28000.(0<x<200);②当a=60时,利润是定值为28000元,此时进货方案是购买m件A种商品,(200﹣m)件B种商品(100≤m≤120).
【解析】
(1)根据等量关系:用2400元购进A种商品的数量与用3000元购进B种商品的数量相同,列出方程即可解决问题.
(2)①根据总利润=A商品利润+B商品利用计算即可解决问题.
②分50<a<60,60<a<70,a=60三种情形,根据一次函数的性质讨论即可解决问题.
(1)由题意得:![]() ,
,
解得:m=80.
∴m=80.
(2)①y=[160﹣(80﹣a)]x+(240﹣100)(200﹣x)
=(a﹣60)x+28000.(0<x<200);
∴y=(a﹣60)x+28000.(0<x<200);
②∵y=(a﹣60)x+28000,100≤x≤120,
∴当50<a<60时,由于a﹣60<0,则y随x增大而减小,
∴x=100时,y有最大值,
此时进货方案是购买100件A种商品,100件B种商品利润最大.
当60<a<70时,y随x增大而增大,
∴x=120时,y有最大值,
此时进货方案是购买120件A种商品,80件B种商品利润最大.
当a=60时,利润是定值为28000元,此时进货方案是购买m件A种商品,(200﹣m)件B种商品(100≤m≤120).


科目:初中数学 来源: 题型:
【题目】如图,长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,动点
的中点,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 的速度沿
的速度沿![]() 运动,最终到达点
运动,最终到达点![]() .若点
.若点![]() 运动的时间为
运动的时间为![]() 秒,那么当
秒,那么当![]() _____________秒时,
_____________秒时,![]() 的面积等于
的面积等于![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点P为正方形边上一动点,若点P从点A出发沿A→D→C→B→A匀速运动一周.设点P走过的路程为x,△ADP的面积为y,则下列图象能大致反映y与x的函数关系的是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②4a+2b+c<0;③a﹣b+c>0;④(a+c)2<b2 . 其中正确的结论是( )
A.①②
B.①③
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
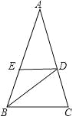
【题目】如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形的个数( )
A. 1个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据阅读内容,在括号内填写推理依据.
如果两条平行线被三条直线所截,那么一对内错角的角平分线一定互相平行.
已知:AB∥CD,EM平分∠AEF,FN平分∠EFD
求证: EM∥FN

证明:
∵AB∥CD
∴∠AEF=∠DFE ( )
∵EM平分∠AEF
∴∠MEF=![]() ∠ AEF ( )
∠ AEF ( )
∵FN平分∠EFD
∴∠EFN=![]() ∠ EFD ( )
∠ EFD ( )
∴∠MEF=∠ EFN
∴ EM ∥FN ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形![]() 的底边
的底边![]() 长为
长为![]() ,面积是
,面积是![]() , 腰
, 腰![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 边于
边于![]() 点.若点
点.若点![]() 为
为![]() 边的中点,点
边的中点,点![]() 为线段EF上一动点,则
为线段EF上一动点,则![]() 周长的最小值为( )
周长的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD在平面直角坐标系中,AD∥BC∥x轴,AB∥DC∥y轴,x轴与y轴夹角为90°,点M,N分别在xy轴上,点A(1,8),B(1,6),C(7,6),D(7,8).

(1)连接线段OB、OD、BD,求△OBD的面积;
(2)若长方形ABCD在第一象限内以每秒0.5个单位长度的速度向下平移,经过多少秒时,△OBD的面积与长方形ABCD的面积相等请直接写出答案;
(3)见备用图,连接 OB,OD,OD交BC于点E,∠BON的平分线和∠BEO的平分线交于点F.
①当∠BEO的度数为n,∠BON的度数为m时,求∠OFE的度数.
②请直接写出∠OFE和∠BOE之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com