Question

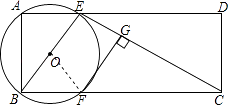
【题目】如图，在矩形ABCD中，AB=2，AD=5，过点A、B作⊙O，交AD，BC于点E，F，连接BE，CE，过点F作FG⊥CE，垂足为G．

（1）当点F是BC的中点时，求证：直线FG与⊙O相切；
（2）若FG∥BE时，求AE的长．

Answer 1

【答案】
（1）证明：连接OF，

∵点F是BC的中点，

∴BF=CF，

在矩形ABCD中，∵∠A=90°，

∴BE是⊙O的直径，

∴BO=OE，

∴OF∥CE，

∵FG⊥CE，

∴OF⊥FG，

∴直线FG与⊙O相切

（2）解：∵FG∥BE，FG⊥CE，

∴BE⊥CE，

∴∠AEB+∠DEC=90°，

∵∠ABE+∠AEB=90°，

∴∠ABE=∠DEC，

∵∠A=∠D=90°，

∴△ABE∽△CDE，

∴ ，

∵AB=2，AD=5，

∴CD=AB=2，

∴ ，

∴AE=1，或AE=4．

【解析】（1）连接OF，由点F是BC的中点，得BF=CF，在矩形ABCD中，∵∠A=90°，得BE是⊙O的直径，求得BO=OE，根据三角形得中位线得OF∥CE，证得OF⊥FG即可；（2）根据平行线的性质得到BE⊥CE，由余角的性质得到∠ABE=∠DEC证得△ABE∽△CDE，根据相似三角形得性质就可求出答案。
【考点精析】关于本题考查的平行线的性质和三角形中位线定理，需要了解两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半才能得出正确答案．