
【题目】“推进全科阅读,培育时代新人”.某学校为了更好地开展学生读书活动,随机调查了九年级50名学生最近一周的读书时间,统计数据如下表:
时间(小时) | 6 | 7 | 8 | 9 | 10 |
人数 | 5 | 8 | 12 | 15 | 10 |
(1)根据上述表格补全下面的条形统计图;
(2)写出这50名学生读书时间的众数、中位数、平均数;
(3)若该校有1000名学生,求最近一周的读书时间不少于7小时的人数?
【答案】(1)见详解;
(2)这50名学生读书时间的众数为9;中位数为8.5;平均数为8.34;
(3)最近一周的读书时间不少于7小时的有900人.
【解析】
(1)根据表格补全条形统计图即可;
(2)根据众数的定义、中位数的定义和平均数公式即可求出结论;
(3)先求出这50名学生中最近一周的读书时间不少于7小时的人数占总人数的百分比,然后用1000乘以这个百分比即可求解;
(1)补全的条形统计图如下:
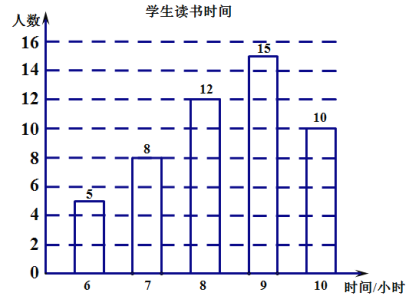
(2)这50名学生读书时间的众数是:9;
中位数是:![]() ;
;
平均数是:![]() ;
;
(3)由统计表可以得到:这50名学生中最近一周的读书时间不少于7小时的人数占总人数的百分比为![]()
![]() 1000名学生中最近一周的读书时间不少于7小时的人数大约为:
1000名学生中最近一周的读书时间不少于7小时的人数大约为:![]() (人)
(人)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc>0;②b<a+c;③当x<0时,y随x的增大而增大;④2c<3b;⑤a+b>m(am+b)(其中m≠1)其中正确的个数是( )
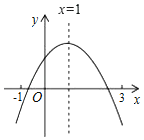
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
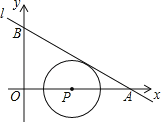
【题目】在直角坐标系中,我们将圆心坐标和半径均为整数的圆称为“整圆”.如图所示,直线l:y=kx+4![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为“整圆”的点P个数是_____个.
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为“整圆”的点P个数是_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为x kg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元, y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
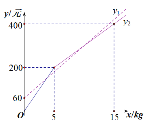
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5 kg后,超过的部分价格优惠是打五折
D.若顾客采摘12 kg草莓,那么到甲园或乙园的总费用相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x的二次函数y=x-bx+![]() b+b-5的图象与x轴有两个公共点.
b+b-5的图象与x轴有两个公共点.
(1)求b的取值范围;
(2)若b取满足条件的最大整数值,当m≤x≤![]() 时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
(3)若在自变量x的值满足b≤x≤b+3的情况下,对应函数y的最小值为![]() ,求此时二次函数的解析式.
,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以![]() 的边
的边![]() 为腰向外作等腰
为腰向外作等腰![]() 和等腰
和等腰![]() ,连
,连![]() 是
是![]() 的中线.
的中线.
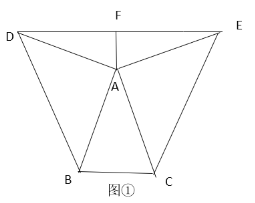
(1)知识理解:图①所示,当![]() 时,则
时,则![]() 与
与![]() 的位置关系为______,数量关系为______;
的位置关系为______,数量关系为______;
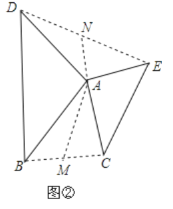
(2)知识应用:图②所示,当![]() 时,M,N分别是BC,DE的中点,求证:
时,M,N分别是BC,DE的中点,求证:![]() 且
且![]() ;
;
(3)拓展提高:图③所示,四边形![]() 中,
中,![]() ,分别以边
,分别以边![]() 和
和![]() 为腰作等腰
为腰作等腰![]() 和等腰
和等腰![]() ,连
,连![]() ,分别取
,分别取![]() 、
、![]() 的中点
的中点![]() ,连
,连![]() .
.
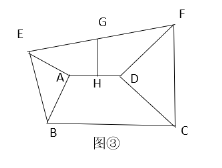
①求证:![]() ;
;
②直接写出![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() .
.
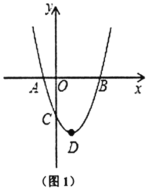
(1)抛物线顶点![]() 的坐标为________;
的坐标为________;
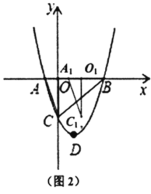
(2)如图2,连接![]() 、
、![]() .将
.将![]() 沿
沿![]() 轴方向以每秒1个单位长度的速度向右平移得到
轴方向以每秒1个单位长度的速度向右平移得到![]() ,运动时间为
,运动时间为![]() 秒.当
秒.当![]() 时,求
时,求![]() 与
与![]() 重叠面积
重叠面积![]() 与
与![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的最大值;
的最大值;
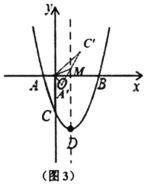
(3)如图3中,将![]() 绕点
绕点![]() 顺时针旋转一定的角度
顺时针旋转一定的角度![]() 得到
得到![]() ,边
,边![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() .在旋转过程中,是否存在一点
.在旋转过程中,是否存在一点![]() ,使得
,使得![]() ?若存在,直接写出所有满足条件的点
?若存在,直接写出所有满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
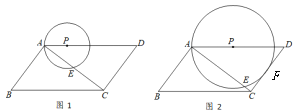
【题目】如图1,平行四边形ABCD中,AB⊥AC,AB=3,AD=5,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1)如图2,当⊙P与边CD相切于点F时,求AP的长;
(2)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”,如10=3+7.
(1)从7,11,13,17这4个素数中随机抽取一个,则抽到的数是11的概率是_____;
(2)从7,11,13,17这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于24的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com