
【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形
(1)求证:△DFB是等腰三角形;
(2)若DA=![]() AF,求证:CF⊥AB.
AF,求证:CF⊥AB.

【答案】(1)△DFB是等腰三角形 (2)见解析
【解析】(1)由AB是⊙O直径,得到∠ACB=90°,由于△AEF为等边三角形,得到∠CAB=∠EFA=60°,根据三角形的外角的性质即可得到结论;
(2)过点A作AM⊥DF于点M,设AF=2a,根据等边三角形的性质得到FM=EN=a,AM=![]() a,在根据已知条件得到AB=AF+BF=8a,根据直角三角形的性质得到AE=EF=AF=CE=2a,推出∠ECF=∠EFC,根据三角形的内角和即可得到结论.
a,在根据已知条件得到AB=AF+BF=8a,根据直角三角形的性质得到AE=EF=AF=CE=2a,推出∠ECF=∠EFC,根据三角形的内角和即可得到结论.
解:(1)∵AB是⊙O直径,
∴∠ACB=90°,
∵△AEF为等边三角形,
∴∠CAB=∠EFA=60°,
∴∠B=30°,
∵∠EFA=∠B+∠FDB,
∴∠B=∠FDB=30°,
∴△DFB是等腰三角形;
(2)过点A作AM⊥DF于点M,设AF=2a,

∵△AEF是等边三角形,∴FM=EN=a,AM=![]() a,
a,
在Rt△DAM中,AD=![]() AF=2a,AM=
AF=2a,AM=![]() ,
,
∴DM=5a,∴DF=BF=6a,
∴AB=AF+BF=8a,
在Rt△ABC中,∠B=30°,∠ACB=90°,∴AC=4a,
∵AE=EF=AF=CE=2a,∴∠ECF=∠EFC,
∵∠AEF=∠ECF+∠EFC=60°,∴∠CFE=30°,
∴∠AFC=∠AFE+∠EFC=60°+30°=90°,
∴CF⊥AB.


科目:初中数学 来源: 题型:
【题目】我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示(图②是备用图),如果把锅纵断面的抛物线记为C1,把锅盖纵断面的抛物线记为C2.
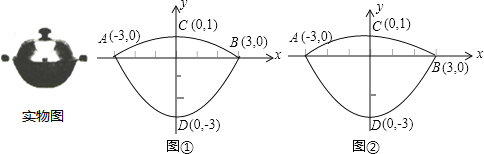
(1)求C1和C2的解析式;
(2)如果炒菜时锅的水位高度是1dm,求此时水面的直径;
(3)如果将一个底面直径为3dm,高度为3dm的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的口袋中,有三张形状、大小、质地完全相同的纸片,三张纸片上分别写有函数:①y=﹣x,②y=﹣![]() ,③y=2x2.
,③y=2x2.
(1)在上面三个函数中,其函数图象满足在第二象限内y随x的增大而减小的函数有 (请填写序号);现从口袋中随机抽取一张卡片,则抽到的卡片上的函数图象满足在第二象限内y随x的增大而减小的概率为 ;
(2)王亮和李明两名同学设计了一个游戏,规则为:王亮先从口袋中随机抽取一张卡片,不放回,李明再从口袋中随机抽取一张卡片,若两人抽到的卡片上的函数图象都满足在第二象限内y随x的增大而减小,则王亮得3分,否则李明得2分,请用列表或画树状图的方法说明这个游戏对双方公平吗?若你认为不公平,如何修改规则才能使该游戏对双方公平呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC的中点,连接AD,在AD的延长线上取一点E,连接BE,CE.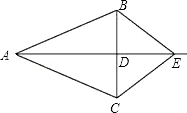
(1)求证:△ABE≌△ACE;
(2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
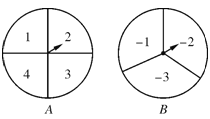
【题目】如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A、B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止.
(1)用画树状图或列表法求乙获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com